
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условие компланарности векторов
Определение 3. Векторы, параллельные одной плоскости, называются компланарными. Очевидно, что два вектора всегда компланарны.
Теорема 2 (критерий компланарности векторов). Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство: Если три вектора компланарны, можно считать, что они лежат в одной плоскости и тогда объем параллелепипеда, построенного на этих векторах, равен нулю, т.е. смешанное произведение равно нулю.
Если наоборот, смешанное произведение равно нулю, то объем параллелепипеда равен нулю и, значит, все векторы параллельны одной плоскости (компланарны) или хотя бы один из них равен нулю, что тоже означает компланарность всех трех векторов.
Другими словами, необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат этих векторов:
 . (6)
. (6)
Пример 1. Найти векторное произведение 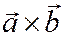 для векторов
для векторов 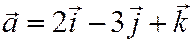 ,
,  .
.
Решение:
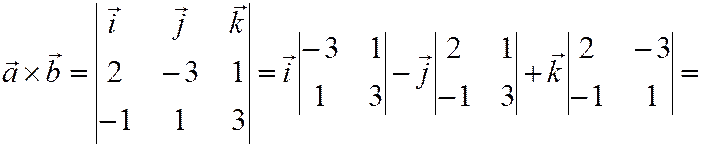
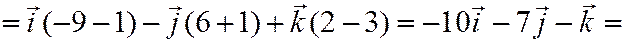
 .
.
Пример 2. Вычислить площадь треугольника АВС, если  ,
,  ,
,  .
.
Решение:  .
.
Так как  ,
,  , то
, то 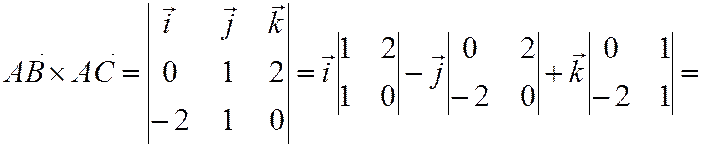
 . Тогда
. Тогда  и
и 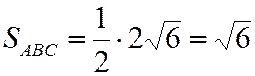 .
.
Пример 3. Упростить выражение:
 .
.
Решение: 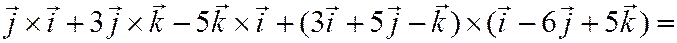
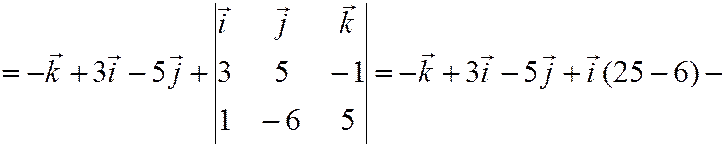
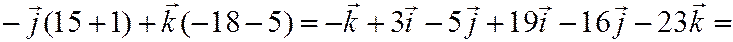
 .
.
Пример 4. В пирамиде ABCD с вершинами A (10,7,1), B (7,10,0), C (1,10,7 ), D (7,1,17) найти:
а) угол между ребрами AB и AD;
б) объем пирамиды.
|
Дата добавления: 2014-01-03; Просмотров: 4294; Нарушение авторских прав?; Мы поможем в написании вашей работы!