Составление математической модели ЗЛП

План

Лекция 3

Тема: Графический метод решения ЗЛП

Цель: научиться составлять математические модели ЗЛП, решать полученные задачи с двумя переменнымиграфическим способом; рассмотреть всевозможные случаи при решении задач графическим способом.

1. Составление математической модели ЗЛП.

2. Графический метод решения ЗЛП.

3. Алгоритм решения ЗЛП.

4. Возможные случаи при решении ЗЛП.

Литература:

1. Н.Ш. Кремер. Исследование операций в экономике.

2. М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложения в экономическом образовании.

3. Сборник задач по высшей математики для экономистов/под ред В.Н.Ермакова

4. Общий курс высшей математики для экономистов: учебник / под ред. В.Н.Ермакова

Чтобы составить математическую модель задачи ЛП, не­обходимо:

— ввести обозначения переменных;

— исходя из цели экономических исследований, составить целевую функцию;

— учитывая ограничения в использовании экономических показателей задачи и их количественные закономернос­ти, записать систему ограничений.

Пример: Озеро можно заселить двумя видами рыб А и В. Средняя масса рыбы равна 2 кг для вида А и 1 кг для вида В. В озере имеется два вида пищи: Р1 и Р₂. Средние потребности одной рыбы вида А составляют 1 ед. корма Р₁ и 3 ед. корма Р₂ в день. Аналогичные потребности для рыбы вида В составляют 2 ед. Р₁ и 1 ед. Р₂. Ежедневный запас пищи поддерживается на уровне 500 ед. Р₁ и 900 ед. Р ₂. Как следует заселить озеро рыбами, чтобы максимизировать общую массу рыб?

Решение. Обозначим х₁ - число рыб вида А

х₂ - число рыб вида В.

Общая масса рыб будет равна L(x) = 2х₁ + х₂.

Корма Р₁ этим рыбам потребуется х₁ + 2х₂ единиц в день. Поскольку дневной запас корма Р₁ ограничен величиной 500 ед., то мы должны ввести ограничение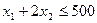

Для корма P₂ получаем аналогично второе ограничение: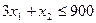

Кроме того, х₁³ 0 и х ₂ ³ 0.

Получили задачу линейного программирования:

L(x) = 2х₁ + х₂ (-» max)

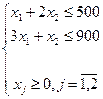
Дата добавления: 2014-01-03