Графический метод решения ЗЛП

Наиболее простым и наглядным методом ЛП является графический метод. Он позволяет решать задачи ЛП в стандартной и неканонической формах, в которых не более двух переменных, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

Решим нашу за­дачу графическим способом. Допус­тимые планы за­дачи располагают­ся в первом квад­ранте, т.к. х₁³ 0, х ₂ ³ 0.

Неравенство 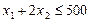определяет полуплоскость, которая содержит точку (0; 0).

Отметим стрелками на чертеже выбранную полуплоскость. Аналогичным образом находим полу­плоскость, заданную неравенством

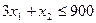
Прямая (l ₂) Зх₁ + х₂ = 900 — граница этой полуплоскости — пересекает координатные оси в точках (300; 0) и (0; 900). Областью допустимых планов будет четырехугольник ОАВС.

Изучим поведение функции цели L(x)=2х₁ + х ₂, для которой мы хотим найти точку максимума.

Строим вектор 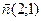, координаты которого есть коэффициенты целевой функции, и который называется градиентом. Он показывает направление наискорейшего изменения целевой функции. Для всех точек какой-либо прямой, перпендикулярной вектору 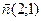, целевая функция имеет одно и тоже значение. Такие прямые называют линиями уровня целевой функции. Все они параллельны друг другу и перпендикулярны вектору 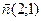.Перемещая параллельно самой себе линию уровня в направлении вектора 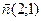, можно найти точку минимума и точку максимума целевой функции. Точкой минимума будет та из точек ОДР, в которой перемещаемая линия уровня впервые встретилась с областью допустимых решений, а точкой максиму­ма — та, в которой линия уровня полностью вышла из области.

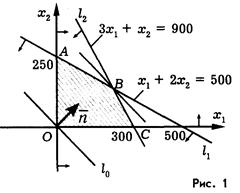
Изобразим на рисунке 1 линию уровня нашей целевой функции. Прямая (L) 2х ₁ + х ₂ = 0 проходит через начало координат и перпендикулярна вектору 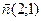. Из рисунка видно, что точкой максимума будет точка В — точка пересечения прямых /₁ и 1 ₂.

Для нахождения координат точки В составляем систему урав­нений, в которую входят уравнения прямых /₁ и 1 ₂:

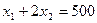
Зх₁ + х₂ = 900

Решением этой системы будет пара чисел: х₁ = 260, х ₂ = 120.

Итак, найден оптимальный план х = (260; 120). В этой точке целевая функция имеет значение L(x)= 2*260 + 120 = 640.

Смысл найденного ответа такой. Наибольшей будет общая масса рыб при условии, если в озере будет 260 рыб вида А и 120 рыб вида В и равна эта масса 640 кг.

Дата добавления: 2014-01-03