То основную гипотезу отклоняют

ПРОВЕРКА НЕПАРАМЕТРИЧЕСКИХ ГИПОТЕЗ

Для проверки гипотезы о виде закона распределения случайной непрерывной величины можно использовать критерии согласия: критерии Пирсона и Колмогорова. Проверку непараметрической гипотезы о виде закона распределения следует проводить при помощи критерия Пирсона (критерия χ²), если распределение дискретное.

Обычно гипотеза о виде закона распределения выдвигается после визуального изучения кумуляты, гистограммы и анализа полученных оценок числовых характеристик.

При проверке основной гипотезы 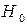с использованием критерия Пирсона для случайной дискретной величины сначала составляют сгруппированный статистический ряд, а затем вычисляют следующую выборочную статистику:

· .

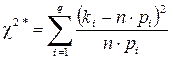В формуле для 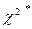— n это объем выборки, k_i — это частота выборочного значения 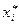, 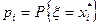— это теоретические (гипотетические) вероятности, которые вычисляются исходя из предположения о виде закона распределения (гипотезы ).

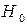Для случайной непрерывной величины сначала строят интервальный статистический ряд, а затем вычисляют выборочную статистику по следующей формуле:

· .

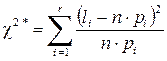Здесь l_i э то частота попадания выборочного значения в интервал с номером i. Вероятности попадания случайной непрерывной величины в интервал с номером i: 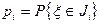, вычисляются по одной из двух формул:

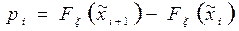· или · .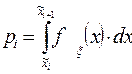

Здесь F_ξ(x), f_ξ(x) это гипотетические функция распределения и гипотетическая плотность распределения соответственно.

При проверке гипотез по критерию Пирсона критическая область будет правосторонней. Её границу к₂ ищут по таблицам критических точек распределения 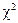по заданному уровню значимост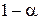и и 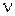степенями свободы из условия 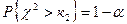. Для случайной дискретной величины число степеней свободы будет равно: 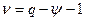, для случайной непрерывной — 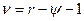, где y — число параметров распределения, оцениваемых по выборке.

Например, если случайная величина распределена по нормальному закону, то у этого распределения два параметра m = E[ξ] и s²=V [ξ]. В том случае, если оба параметра оценивались по выборке, то y=2. У случайной величины, распределенной по показательному закону, один параметр λ=1/E[ξ], поэтому, y=1, если этот параметр оценивался с использованием выборочной информации. Равномерный закон распределения на отрезке [а; b] характеризуется двумя параметрами: границами этого отрезка, значит, если они оценивались по выборке, то y=2.

Если 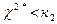, то гипотеза 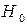принимается, если 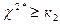, то основная гипотеза отвергается.

При проверке гипотезы по критерию Пирсона для случайной дискретной величины следует иметь в виду, что если частота повторения выборочного значения 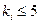, а для непрерывной случайной величины частота попадания в интервал 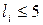, то в первом случае, требуется объединить указанное значение с любым соседним. Во втором случае, для непрерывной случайной величины, следует объединить интервал 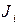с любым соседним.

При проверке гипотезы 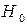о виде закона распределения случайной непрерывной величины по критерию согласия Колмогорова вычисляют следующую выборочную статистику

· .

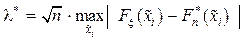Для этого предварительно находят эмпирическую функцию распределения и вычисляют значения гипотетической (предполагаемой) функции распределения в концах интервалов. Затем находят абсолютную величину разницы значений обеих функций на концах интервалов и выбирают наибольшую из них.

Критическая область является правосторонней, и её границу ищут по таблицам распределения Колмогорова по уровню значимости 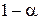. Если 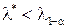, то гипотеза 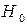принимается, если 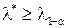, то основная гипотеза отвергается и принимается альтернативная гипотеза.

Одной из задач статистической проверки гипотез, является задача проверки гипотез об однородности двух выборок. Предположим, что мы изучаем две с.в. ξ₁ и ξ₂ и у нас есть основания предполагать, что у этих случайных величин один и тот же закон распределения. Для проверки этого предположения можно использовать критерий Колмогорова-Смирнова, который позволяет проверять гипотезу о том, что две выборки однородны, то есть, извлечены из одной и той же генеральной совокупности.

Для каждой из двух выборок объема n₁ и n₂ соответственно, строят интервальные статистические ряды и находят эмпирические функции распределения 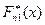и 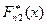. Затем вычисляют значение Z^* по формуле:

· .

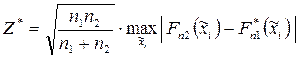Если изучаемые случайные величины имеют одинаковое распределение, (то есть, если основная гипотеза верна), то критерий Z^* будет иметь распределение Колмогорова. Границу критической области к₂, которая будет являться правосторонней, находят по таблицам распределения Колмогорова по заданному уровню значимости. Если 0 < Z^*<к₂, то принимают гипотезу о том, что обе случайные величины имеют одинаковый закон распределения, если указанное неравенство нарушается, то принимают альтернативную гипотезу.

В пакете Stata при тестировании гипотез также выводится величина р-value, соответствующая той выборочной статистике, которую вычисляют для проведения теста. Рассмотрим, как реализуется в Стате алгоритм проверки гипотезы о законе распределения.

Дата добавления: 2014-01-03