
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 3. Определение. Маршрутом длины на графе называется такая последовательность
|
|
|
|
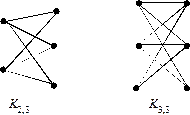
3.2. Маршруты, цепи и циклы в графе
Определение. Маршрутом длины 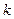 на графе
на графе 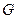 называется такая последовательность
называется такая последовательность 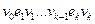 вершин и ребер графа, в которой
вершин и ребер графа, в которой 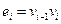
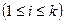 .
.
Такой маршрут кратко называют 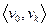 - маршрутом и кратко обозначают
- маршрутом и кратко обозначают 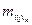 . Про
. Про 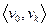 - маршрут говорят, что он соединяет вершину
- маршрут говорят, что он соединяет вершину 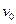 с вершиной
с вершиной 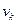 . Вершины
. Вершины 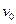 и
и 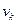 называют соответственно началом и концом маршрута.
называют соответственно началом и концом маршрута.
Случай, когда длина маршрута равна нулю, не исключается; в этом случае маршрут сводится к одной вершине.
Если 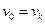 , то маршрут называется замкнутым.
, то маршрут называется замкнутым.
Заметим, что в обыкновенном графе маршрут полностью определяется последовательностью 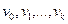 своих вершин.
своих вершин.
В произвольном маршруте любое ребро и любая вершина могут повторяться. Накладывая ограничения на число повторений вершин и ребер, приходим к следующим частным видам маршрутов.
Определение. Цепь – это маршрут без повторяющихся ребер.
Цепь, соединяющую вершину 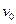 с вершиной
с вершиной 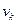 , кратко называют
, кратко называют 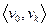 - цепью и обозначают
- цепью и обозначают 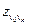 .
.
Определение. Цепь называется простой, если в ней нет повторяющихся вершин за исключением, быть может, совпадающих концевых.
Определение. Замкнутая цепь называется циклом.
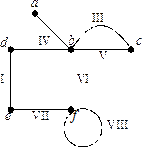 Определение. Замкнутая простая цепь называется простым циклом.
Определение. Замкнутая простая цепь называется простым циклом.
Пример 1. 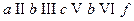 -
- 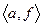 - маршрут; его длина равна 4; данный маршрут является
- маршрут; его длина равна 4; данный маршрут является 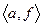 - цепью; эта цепь незамкнутая, не простая. Маршрут
- цепью; эта цепь незамкнутая, не простая. Маршрут 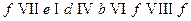 - цикл длины 5, этот цикл не является простым;
- цикл длины 5, этот цикл не является простым; 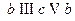 - простой цикл.
- простой цикл.
3.3. Связность, компоненты связности графа
Определение. Обозначим через Gi подграф графа G, порожденный множеством вершин Vi. При этом 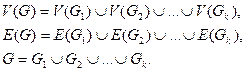
Графы 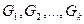 называют компонентами связности графа G.
называют компонентами связности графа G.
Определение. Число различных компонент связности графа 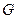 называется числом связности и обозначается
называется числом связности и обозначается 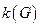 .
.
Определение. Если 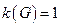 , то граф называется связным.
, то граф называется связным.
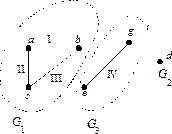 Пример 1. Рассмотрим граф
Пример 1. Рассмотрим граф 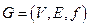 , с множеством вершин
, с множеством вершин 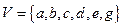 , множеством ребер
, множеством ребер 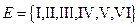 и отображением инцидентности:
и отображением инцидентности: 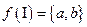 ,
, 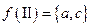 ,
, 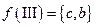 ,
, 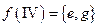 . Имеем три компоненты связности:
. Имеем три компоненты связности:
1. 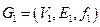 , где
, где 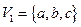 ,
, 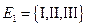 ,
, 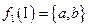 ,
, 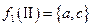 ,
, 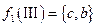 ;
;
2. 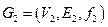 , где
, где 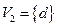 ,
, 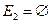 ;
;
3. 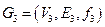 , где
, где 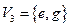 ,
, 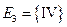 ,
, 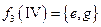 .
.
3.4. Цикломатическое число графа
Пусть 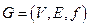 - произвольный граф;
- произвольный граф; 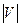 - число его вершин,
- число его вершин, 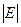 - число ребер,
- число ребер, 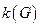 - число связности.
- число связности.
Определение. Поставим графу 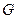 в соответствие число
в соответствие число 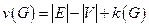 , называемое цикломатическим числом графа.
, называемое цикломатическим числом графа.
3.5. Матрицы, ассоциированные с графом
Во многих задачах теории графов (особенно реализуемых на ЭВМ) графы удобно описывать матрицами. Пусть 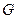 - произвольный неориентированный граф с m вершинами и n ребрами. Занумеруем вершины графа.
- произвольный неориентированный граф с m вершинами и n ребрами. Занумеруем вершины графа.
Определение. Матрицей смежности неориентированного графа 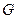 называется матрица
называется матрица 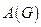 размера
размера 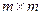 , элементы которой
, элементы которой 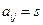 , где
, где 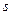 - число ребер, соединяющих вершины с номерами
- число ребер, соединяющих вершины с номерами 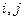 , причем при
, причем при 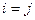 каждую петлю учитываем дважды.
каждую петлю учитываем дважды.
Замечание. Для каждого графа имеется несколько матриц смежности, отвечающих различным упорядочениям множества вершин графа. Очевидно, что одна такая матрица смежности получается из другой с помощью некоторой перестановки строк и аналогичной перестановки столбцов.
Помимо вершин занумеруем ребра графа.
Определение. Матрицей инцидентности неориентированного графа 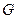 называется матрица
называется матрица 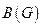 размера
размера 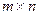 , элементы которой
, элементы которой 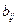 определены следующим:
определены следующим:
1. 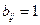 , если вершина с номером i инцидентна ребру с номером j и j-ое ребро не является петлей;
, если вершина с номером i инцидентна ребру с номером j и j-ое ребро не является петлей;
2. 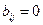 во всех остальных случаях.
во всех остальных случаях.
Замечание. Для каждого графа имеется несколько матриц инцидентности, отвечающих различным упорядочениям множества вершин и ребер графа. Очевидно, что одна такая матрица инцидентности получается из другой с помощью некоторой перестановки строк и некоторой перестановки столбцов.
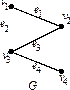 Пример.
Пример. 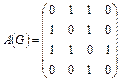 ;
; 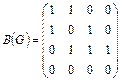 .
.
3.6. Деревья и леса
Определение. Граф без циклов, называется ациклическим графом или лесом.
Определение. Связный ациклический граф называется деревом.
Каждая компонента связности леса – дерево, следовательно, для 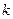 -связного леса существует дизъюнктное разбиение на
-связного леса существует дизъюнктное разбиение на 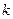 деревьев.
деревьев.
Пример 1. Граф  не является деревом, не является лесом. Граф
не является деревом, не является лесом. Граф  - дерево. Граф
- дерево. Граф  - лес.
- лес.
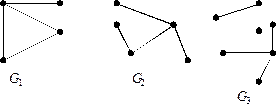
Теорема. Связный граф 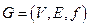 является деревом тогда и только тогда, когда
является деревом тогда и только тогда, когда 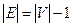 .
.
Следствие. Если граф 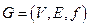 -
-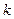 -связный лес, то
-связный лес, то 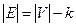 .
.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 528; Нарушение авторских прав?; Мы поможем в написании вашей работы!