Кодирование деревьев

Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называется корневым.

Для задания (с точностью до изоморфизма) корневых деревьев используют код из 0 и 1, который мы определим индуктивно.

Определение. Кодом корневого дерева с одним ребром является 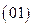. Пусть деревья 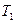и 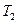с корнями a и b соответственно (см. рис.) имеют коды 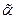и 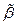. Тогда кодом дерева 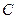с корнем с является код 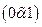, а кодом дерева 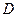с корнем 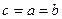- код .

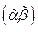Пример 1. Написать код дерева, изображенного на рисунке.

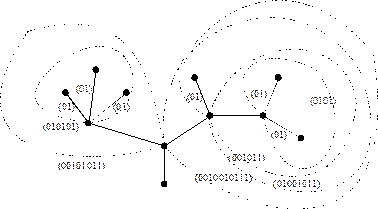
Итак, код дерева - .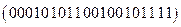

Справедливо следующее утверждение: для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева необходимо и достаточно, чтобы число нулей и единиц в этой последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.

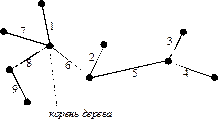Чтобы построить корневое дерево по коду из нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшаяся в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками, то каждая такая скобка будет соответствовать ребру графа.

Пример 2. Построить дерево по коду

.

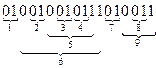Для задания помеченных деревьев, т.е. деревьев, вершины которых занумерованы, используют код из натуральных чисел.

Пусть дано помеченное дерево. Чтобы построить его код из натуральных чисел действуем следующим образом. Находим висячую вершину с наименьшим номером. Записываем номер смежной с ней вершины (это начало кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находим висячую вершину с наименьшим номером, записываем номер смежной с ней вершины (это продолжение кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Так поступаем до тех пор, пока не останется последнее ребро.

Заметим, что длина кода из натуральных чисел на единицу меньше числа ребер и на две единицы меньше числа вершин данного дерева.

Пример 3. На рисунке изображено помеченное дерево. Его код .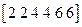

Построение дерева по коду из натуральных чисел рассмотрим на примере кода 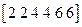. Прежде всего, заметим, что дерево, которое нам предстоит построить, имеет 8 вершин.

Будем преобразовывать последовательность 224466, действуя по следующей схеме. Вместо первого числа запишем наименьшее натуральное число, которое в этой последовательности не встречается, т.е. 1; получим последовательность 124466. Вместо второго числа в новой последовательности запишем наименьшее, не встречающееся в ней, т.е. 3; получим последовательность 134466, и т.д. Действуем так до тех пор, пока все числа в исходной последовательности не будут заменены. Расположим все последовательности друг под другом; под последней из них запишем код дерева. Выпишем пары вершин, записанные друг под другом в последних двух строчках: (12), (32), (24), (54), (46), (76). Каждая такая пара - это пара концов одного из ребер дерева. Этот список дополняем парой вершин, отсутствующих в предпоследней строчке, т.е. парой (6,8). Теперь строим дерево: отмечаем на плоскости точки – вершины дерева и соединяем их ребрами согласно списку (см. рисунок к примеру 3).

3.8. Эйлеровы графы

Определение. Цикл на графе 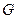называется эйлеровым циклом, если он содержит все вершины и все ребра графа.

Определение. Граф, на котором имеется эйлеров цикл, называется эйлеровым графом.

Пример 1. Рассмотрим граф 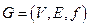: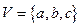, , 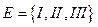, , 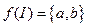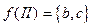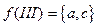. Цикл 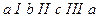эйлеров. Следовательно, 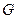- эйлеров граф.

Лемма. Если степень каждой вершины связного графа 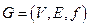четна, то он содержит хотя бы один цикл.

Теорема (критерий эйлеровости графа). Ненулевой граф является эйлеровым в том и только в том случае, если он связен и каждая его вершина имеет четную степень.

Пример 2. Свое название эйлеровы графы получили в честь Л. Эйлера, который первым рассмотрел такие графы в 1736 году в своей знаменитой работе о кенигсбергских мостах. Задача эта состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рисунке 1. Спрашивается, можно ли, начиная с некоторого места суши, обойти все мосты по одному разу и вернуться назад?

Эйлер предложил рассмотреть граф, изображенный на рисунке 2. В итоге решение задачи о кенигсбергских мостах свелось к поиску эйлерового цикла на графе. Согласно доказанной теореме такого цикла на графе нет, поскольку степени вершин этого графа нечетные.

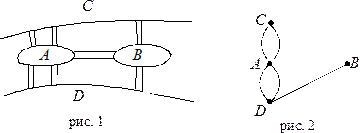
3.9. Раскраска графа

Пусть 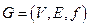- произвольный граф и 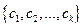- некоторое множество, элементы которого будем называть красками.

Определение. Раскраской графа 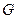в 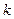цветов называется отображение 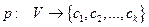такое, что для любых двух смежных вершин 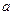и 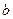выполняется .

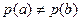Будем говорить, что вершина 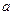имеет цвет .

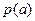Отметим, что здесь не предполагается, что 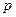отображает 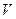на все множество красок .

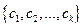Граф называется 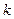- раскрашиваемым, если он может быть раскрашен в 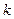цветов. Если при этом его нельзя раскрасить в 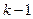цвет, то он называется 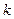- хроматическим. Число 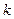в таком случае называют хроматическим числом графа и обозначают .

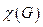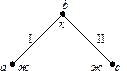Пример 1. Рассмотрим граф 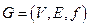: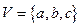, , 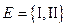, 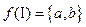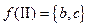. Поскольку в графе есть смежные вершины, то раскрасить его в один цвет нельзя. Пример раскраски этого графа в два цвета: вершину 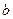красим в красный цвет, а вершины 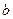и 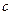- в желтый. Следовательно, хроматическое число графа .

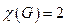Заметим, что хроматическое число любого нулевого графа, т.е. графа, множество ребер которого пусто, равно 1.

Граф, хроматическое число которого равно двум, называется бихроматическим.

Утверждение. Если наибольшая из степеней вершин обыкновенного граф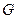а равна 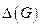, то .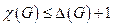

3.10. Планарные графы

Напомним, что граф называется планарным, если существует правильная геометрическая реализация этого графа на плоскости. Правильные геометрические реализации планарного графа на плоскости будем называть плоскими графами.

Теорема 1. Пусть 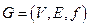- плоский граф, 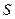- множество его граней. Тогда

.

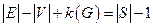Следствие. Пусть 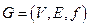- плоский связный граф и 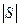- число его граней. Тогда справедлива формула Эйлера

.

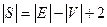Теорема. Любой планарный граф можно раскрасить не более чем четырьмя красками.

3.11. Ориентированные графы

Определение. Пусть 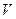- конечное непустое множество (назовем его множеством вершин); 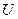- конечное множество (назовем его множеством дуг); 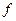- отображение множества 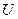в 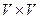(назовем его отображением инцидентности). Тройку 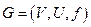называют ориентированным графом или, короче, орграфом.

Элементы множества 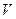называют вершинами, а элементы множества 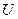- дугами.

Пусть вершины 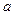, 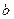и дуга 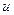таковы, что 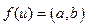. В этом случае будем также писать 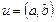. Вершину 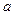называют началом дуги 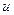, а вершину 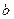- ее концом. При этом говорят, что дуга 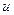исходит (выходит) из вершины 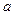и заходит в вершину 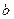. Дуга 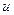и вершина 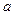(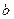) называются при этом инцидентными.

Число дуг, выходящих из вершины 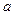, называется полустепенью исхода вершины 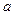и обозначается 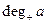. Число дуг, заходящих в вершину 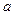, называется полустепенью захода вершины 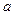и обозначается 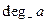. Число 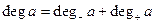называется степенью вершины .

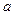Понятие изолированных и висячих вершин, кратных дуг и петель вводится для орграфов так же, как и для неориентированных графов.

Лемма. Пусть 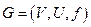- произвольный орграф. Тогда

.

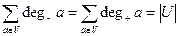Это утверждение аналогично лемме о рукопожатиях, рассмотренной нами в параграфе 3.1. для неориентированных графов; его часто называют орлеммой о рукопожатиях.

Определение. На множестве орграфов введем бинарное отношение, называемое отношением изоморфизма, которое определим следующим образом: будем говорить, что орграфы 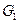и 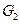связаны отношением изоморфизма, если существует пара взаимно однозначных отображени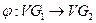й и 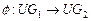таких, что для любой дуги 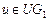выполнено условие:

.

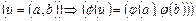Орграфы 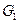и 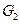, связанные отношением изоморфизма, называют изоморфными и пишут .

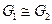По аналогии с понятием геометрического неориентированного графа вводится понятие геометрического орграфа, а также понятие геометрической реализации (диаграммы) орграфа. Разница состоит лишь в том, что отрезкам непрерывных кривых, изображающим дуги, придают направление.

С каждым орграфом 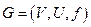естественно связать неориентированный граф 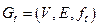, называемый основанием данного графа. Для получения основания необходимо каждую дугу 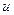графа 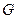заменить на такое ребро 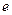, что если 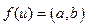, то .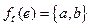

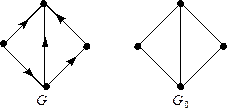
Пример 1. На рисунках изображен ориентированный граф 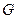и его основание .

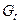Определение. Орграф называется связным, если связно его основание.

Определение. Путем длины 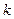на орграфе 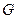называется последовательность вершин и дуг

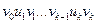
такая, что для любой дуги 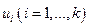вершина 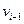является началом, а вершина 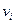- концом.

Про такой путь говорят, что он соединяет вершины 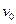с 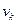, кратко называют 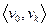- путем; вершины 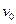и 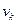называют при этом соответственно началом и концом пути.

Определение. Матрицей смежности орграфа 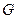называется матрица 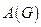размера 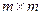, элементы которой 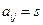, где 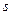- число дуг, исходящих из вершины с номером 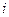и заходящих в вершину с номером .

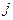Определение. Матрицей инцидентности орграфа 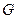называется матрица 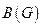размера 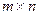, элементы которой 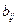определены следующим:

1. 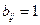, если вершина с номером i – начало дуги с номером j и j-ая дуга – не петля;

2. 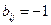, если вершина с номером i – конец дуги с номером j и j-ая дуга – не петля;

3. 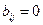во всех остальных случаях.

Дата добавления: 2014-01-03