Пример 3

;

.

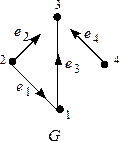
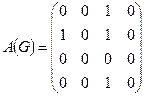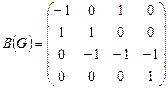3.12. Задача о кратчайшем пути

Определение. Взвешенный связный орграф 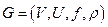называется сетью.

Пусть на графе 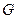имеется путь 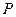из вершины 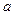в вершину 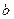и 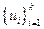- последовательность дуг этого пути. Число 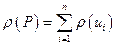называется весом или длиной пути .

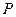Наименьшую из длин 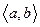-путей назовем расстоянием от 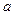до 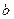, а тот 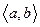-путь, длина которого равна расстоянию от 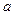до 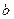, будем называть кратчайшим 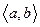-путем.

Задача о кратчайшем пути состоит в следующем: в заданной сети 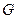найти расстояние и кратчайший путь от фиксированной вершины 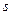до остальных вершин.

Рассмотрим алгоритм Дейкстры, позволяющий решить задачу о кратчайшем пути.

Для удобства изложения введем ряд условных обозначений. Если существует хотя бы один путь из вершины 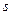в вершину 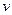, то расстояние от 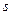до 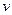будем обозначать через 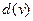. Каждой паре вершин 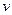и 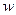будем ставить в соответствие число 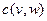, полагая его равным весу дуги, исходящей из 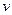и заходящей в 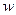, если таковая существует. Если же такой дуги в графе нет, то полагаем .

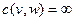Будем говорить, что вершина 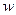ближайшая к вершине 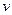из подмножества 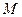множества вершин графа, если расстояние от 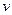до 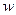является наименьшим из расстояний от вершины 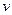до других вершин из множества .

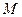В основе алгоритма Дейкстры лежит принцип жадности, заключающийся в последовательном вычислении расстояний сначала до ближайшей к 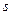вершине, затем до следующей ближайшей и т.д.

Алгоритм Дейкстры. 0-ой шаг. Находится первая ближайшая к вершине 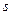вершина: такой вершиной является сама вершина 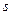, для которой .

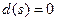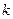-ый шаг. Пусть к началу шага определены 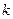вершин, ближайшие к вершине 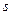, т.е. определено множество 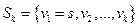, и для всех этих вершин вычислены расстояния 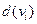,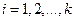. Обозначим через 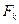множество .

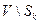Если множество 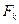пусто, то все возможные расстояния от фиксированной вершины 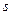до остальных вершин определены на 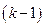-ом шаге.

В противном случае из равенства для каждой вершины 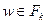положим

.

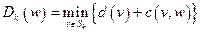Если ни для одной вершины 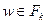этот минимум определить нельзя, то все возможные расстояния от фиксированной вершины 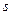до остальных вершин определены на 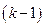-ом шаге.

В противном случае из равенства

,

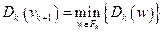определится вершина 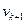, ближайшая к вершине 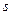из вершин подмножества 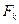, причем

.

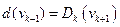Таким образом, по окончании 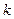-го шага множество вершин, до которых от вершины 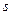вычислено расстояние, расширяется на один элемент.

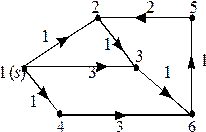Восстановление кратчайшего пути. Кратчайший путь от вершины 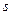до вершины 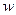восстанавливается пошагово, начиная с вершины 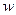до возврата к вершине 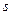. Опишем один шаг возвращения. Для вершины 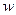среди всех вершин 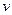, для которых существует дуга, ведущая из 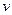в 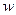, находится такая дуга, для которой выполнено условие 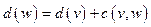. Тем самым восстанавливается последняя дуга кратчайшего пути от 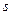до .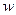

Пример 1. В графе, изображенном на рисунке, найти расстояние от вершины 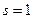до остальных вершин и восстановить кратчайший путь от вершины 1 до вершины 5.

k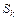
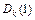
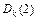
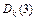
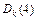
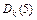
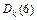
	{1}
	{1,2}
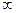
	{1,2,4}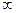
	{1,2,4,3}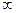
	{1,2,4,3,6}

Кратчайший путь от первой вершины до пятой вершины проходит последовательно через вершины 1,2,3,6,5.

3.13. Задача о максимальном потоке

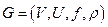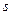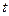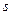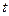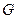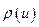В этом параграфе будут рассматриваться сети , имеющие единственную вершину с нулевой полустепенью захода и единственную вершину с нулевой полустепенью исхода. Вершину будем называть источником, а вершину - стоком сети . Вес дуги 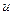будем называть пропускной способностью этой дуги.

Для удобства изложения введем следующие обозначения. Через 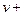обозначим множество дуг, для которых вершина 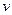является началом, а через 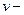обозначим множество дуг, для которых вершина 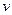является концом.

Определение. Потоком в сети 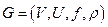называется функция 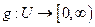, удовлетворяющая условиям:

1. ;

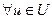
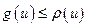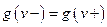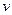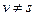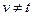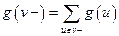2. для всех вершин , , , где и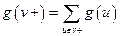

Значение 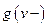можно интерпретировать как поток, втекающий в вершину 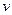, а значение 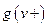- как поток, вытекающий из вершины 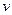. Тогда второе условие можно переформулировать так: поток, втекающий в любую вершину, за исключением источника и стока, должен быть равен вытекающему из этой вершины потоку.

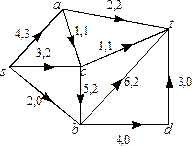Условие 1) называется условием ограничения по пропускной способности, а условие 2) – условием сохранения потока в вершинах.

Пример 1. На рисунке дан пример сети и потока 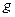в ней. Пропускная способность дуги 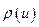указана около соответствующей дуги, там же через запятую указано значение .

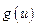Определение. Положим 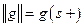. Число 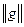называется величиной потока.

Определение. Поток 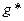называется максимальным, если для любого потока 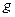справедливо неравенство .

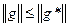Задача о максимальном потоке состоит в следующем: в заданной сети 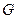найти поток максимальной величины.

Задача о максимальном потоке имеет одну особенность, отличающую ее от рассмотренных нами ранее задач дискретной оптимизации. В предшествующих задачах искомый объект существовал очевидным образом и в принципе мог быть найден полным перебором. Например, можно было перебрать все остовы и выбрать среди них минимальный или перебрать все пути между заданными вершинами и выбрать среди них кратчайший. В задаче о максимальном потоке полный перебор принципиально невозможен и существование максимального потока не является очевидным. Тем не менее, справедлива следующая теорема, которую мы приведем без доказательства.

Теорема. В каждой сети существует максимальный поток.

Определение. Цепью из вершины 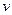в вершину 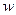на сети 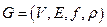называется последовательность попарно различных вершин и дуг

,

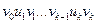(здесь 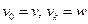), в которой любые два соседних элемента инцидентны.

Если при этом дуга 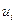выходит извершины 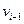и заходит в вершину 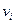, то она называется прямой дугой цепи. Если же дуга 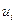выходит извершины 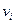и заходит в вершину 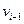, то она называется обратной дугой цепи.

Пусть 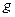- поток в сет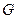и и 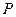- цепь из 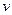в 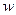. Для каждой дуг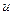и цепи 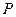положим

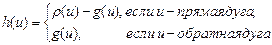
и

.

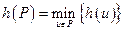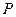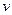Определение. Цепь из в 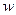называется 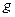- дополняющей, если .

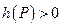Пример 2. В сети, изображенной на рисунке 1, цепь, включающая последовательно вершины 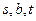, является 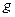- дополняющей для потока, рассмотренного в примере 1.

Одним из алгоритмов, позволяющих построить максимальный поток, является алгоритм Форда-Фалкерсона.

Алгоритм Форда –Фалкерсона. 0-ой шаг. Положим 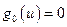для всех дуг .

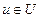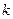-ый шаг. Пусть к началу шага по цепи течет поток 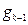. Для текущего потока 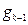ищется 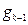-дополняющая 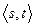-цепь.

Если такой цепи нет, то максимальный поток найден: это .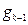

В противном случае, если такая 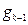-дополняющая 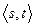-цепь имеется, ей дается имя 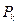и по следующему правилу строится поток :

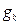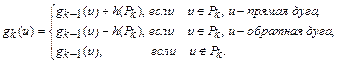
Величина этого потока определяется равенством

.

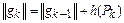Замечание. Возникает существенный вопрос: закончится ли работа алгоритма за конечное число шагов? Оказывается, гарантии этому нет. Гарантировать построение максимального потока можно в случае, если на каждом шаге производить увеличение потока вдоль кратчайших по числу дуг 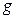-дополняющих цепей.

Пример 3. Построим максимальный поток для сети из примера 1.

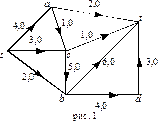Шаг 0. ;

поток указан на рис. 1;

.

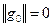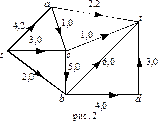
Шаг 1. ,

,

поток 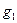указан на рис. 2;

.

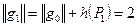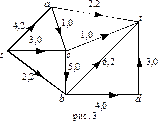Шаг 2. ,

,

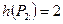поток 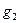указан на рис. 3;

.

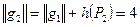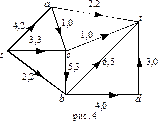Шаг 3. ,

,

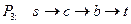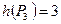поток 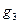указан на рис. 4;

.

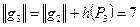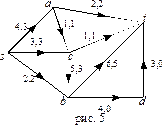
Шаг 4. ,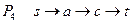

,

поток указан на рис. 5;

.

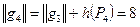Для цепи, изображенной на рисунке 5, 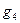-дополняющих цепей из 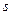в 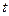нет. Следовательно, поток 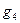является максимальным потоком.

Дата добавления: 2014-01-03