КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямые, перпендикулярные плоскостям проекций, называются проецирующими
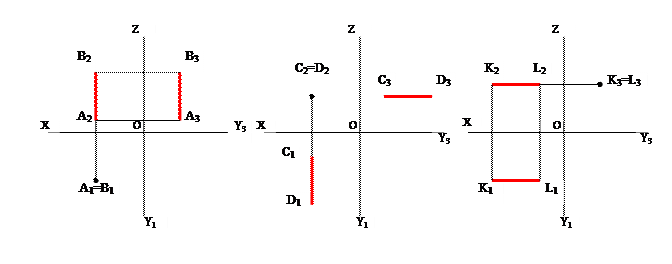
Прямая, ┴ П1, называется горизонтально-проецирующей прямой. На плоскость П1 проецируется в точку, на П2 и П3 в натуральную величину отрезками II оси OZ.
Прямая, ┴ П2, называется фронтально-проецирующей прямой. На плоскость П2 проецируется в точку, на П1 и П3 в виде отрезков натуральной величины, параллельных осям OY1и OY3.
Прямая, ┴ П3, называется профильно-проецирующей прямой. На плоскость П3 проецируется в точку, на П1 и П2 в виде отрезков натуральной величины, параллельных оси ОХ.
Характеристика проецирующих прямых:
1. Проецирующие прямые изображаются на одной из плоскостей проекций, к которой они перпендикулярны, в виде точки, на двух других - в виде вертикальных или горизонтальных отрезков, равных натуральной величине отрезка прямой.
2. Проецирующие прямые составляют с одной из плоскостей проекций угол=90°,с двумя другими углы = 0°
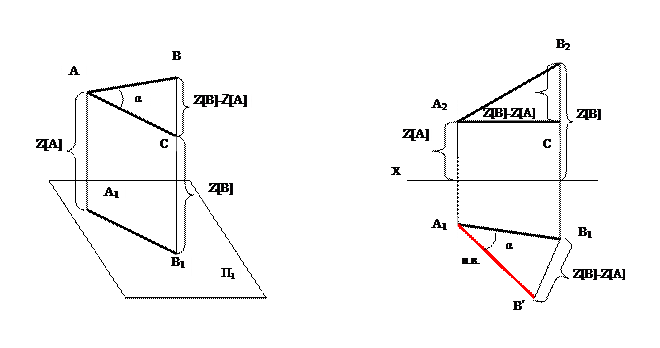Дан отрезок прямой АВ – прямой общего положения. Необходимо определить натуральную величину этого отрезка.
При проецировании на плоскость отрезок имеет искаженную величину, следовательно, А1В1<АВ. Проецирующие лучи АА1 и ВВ1 ┴ П1. Проведя АС′II А1В1, получим прямоугольный ∆АВС с прямым углом АСВ. В этом треугольнике АС′= А1В1 – катет, натуральная величина АВ – гипотенуза, а второй катет ВС′ можно определить как разность координат z точек А и В (zА - zВ).
На основании этих рассуждений определим на комплексном чертеже по проекциям отрезка его натуральную величину.
Натуральная величина отрезка определяется способом прямоугольного треугольника: н.в. отрезка на комплексном чертеже – это гипотенуза прямоугольного треугольника, первый катет которого равен одной из проекций отрезка, а второй катет равен разности расстояний от концов отрезка до той плоскости проекций, на которой взят первый катет.
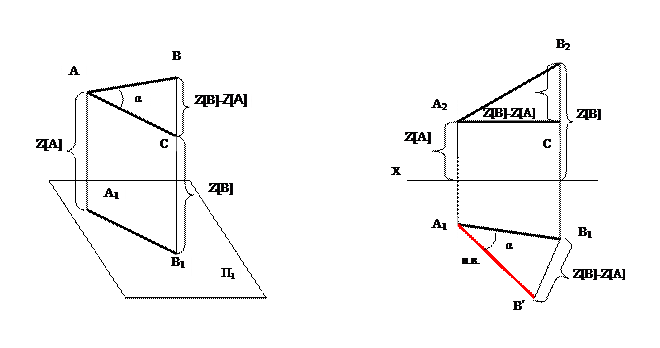Как видно из рисунка, угол наклона прямой АВ к плоскости П1 - это угол ВАС, а на комплексном чертеже это угол В1А1В′, т.е. угол, образованный горизонтальной проекцией А1В1 и гипотенузой АВ прямоугольного треугольника В1А1В′- угол α.
Натуральная величина β и γ наклона прямой АВ к плоскостям П2 и П3 определяется, если прямоугольные треугольники построить соответственно взяв первыми катетами фронтальную проекцию (для определения β) или профильную проекцию (для определения γ).
Углы обозначаются заглавными буквами греческого алфавита α,β,γ
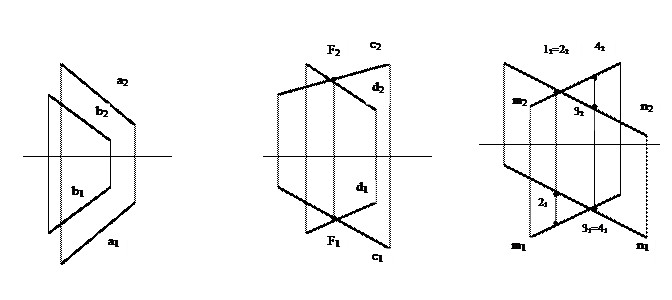Пересекающимися называются прямые, лежащие в одной плоскости и имеющие общую точку.
Скрещивающиеся прямые – прямые, которые не параллельны, не пересекаются, не лежат в одной плоскости.
Характеристики прямых:
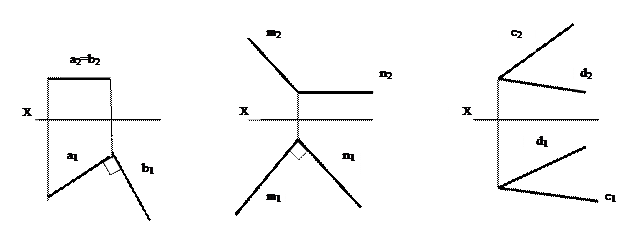
1. Одноименные проекции взаимно параллельных прямых параллельны между собой. Если a II b, то a1 II b1, a2 II b2, a3 II b3.
2. Если прямые пересекаются, то их одноименные проекции также пересекаются, причем проекции точки пересечения лежат на одной линии связи. Если c ∩ d=F, то c1∩d1=F1, и c2∩d2=F2. F1F2┴OX.
3. Если прямые скрещиваются, то точки пересечения одноименных проекций не лежат на одной линии связи
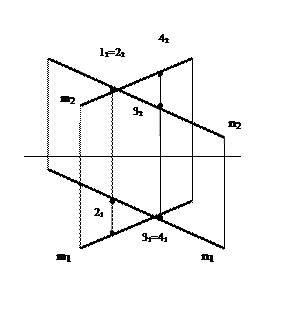Из этих двух точек видимой будет та, которая дальше удалена от плоскости проекции, т.е. находится ближе к наблюдателю.
Из двух горизонтально-конкурирующих точек на П1 видна та точка, которая расположена выше.
Из двух фронтально-конкурирующих точек на П2 видна та точка, которая расположена ближе (по отношению к наблюдателю, стоящему лицом к плоскости П2).
Из двух профильно-конкурирующих точек на П3 видна та точка, которая расположена левее.