Тормозное излучение и поглощение

Рассмотрим свободно-свободные переходы. Тормозное излучение электронов одно из основных причин излучения плазмы в непрерывном спектре (“континууме”). Найдем спектр тормозного излучения исходя из чисто качественных соображений. Сначала вычислим высокочастотную асимптотику классического спектра рассеяния электронов, имеющих скорость u, на точечном кулоновском центра с зарядом Ze (формула Крамерса). Вычисленный для всех w спектр примем за эталонный. Затем введем так называемый фактор Гаунда g (w), который позволяет получить истинный спектр, учитывающий, что электрон взаимодействует с экранированным ядром. Поскольку, электрон может проникать внутрь электронной оболочки рассеивающего иона, то эффективное зарядовое число при рассеянии должно лежать в пределах Z_i << Z_eff < Z. Высоким частотам в спектре соответствуют, очевидно, близкие пролеты r << a, где a = Ze² / mu² – характерная “кулоновская” длина. При этом излучаемая частота w_eff оказывается по порядку величины равной угловой скорости вращения электрона вблизи иона ~ w_rot. Используя законы сохранение энергии и момента импульса

; (7.3)

mur = mu_maxr₀ (7.4) и пренебрегая для близких пролетов левой частью в (7.3), получаем

u_max = ru / r₀; (7.5)

mr²u² / 2(r₀)² = Ze² / r₀; (7.6)

. (7.7) Частоту вращения электрона в точке наибольшего сближения можно записать в виде

, (7.8) где

(7/9) представляет собой характерную частоту спектра излучения, соответствующую прицельному расстоянию r = a.

Энергию, излучаемую в дипольном приближении электроном, имеющим скорость u и пролетающим мимо иона с прицельным расстоянием r, можно оценить следующим образом:

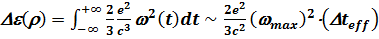, (7.10) где максимальное ускорение электрона равно

, (7.11) а характерное время пролета можно оценить как

. (7.12) Используя (7.5), (7.7), (7.11) и (7.12), получим

, (7.13) что позволяет записать энергию в следующем виде:

. (7.14) Домножив энергию на соответствующее дифференциальное сечение, получим величину

, (7.15) имеющую размерность [эрг×см²]. Если умножить эту величину на поток электронов n_eu_e и плотность ионов n_i, получится мощность тормозного излучения из единицы объема для электронов с прицельным расстоянием r и скоростью u: 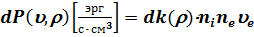. (7.16)

Используя введенное выше приближение

, (7.17) нетрудно перейти от переменной r к w

. (7.18) Заменив величину 4 p ее приближенным числовым значением4p» 12, получим выражение

, (7.19) которое не зависит от частоты.

Строгая классическая теория дает для спектральной интенсивности ту же зависимость, но уже с дополнительным коэффициентом ;

. (7.20) Эта формула называется формулой Крамерса. Физический смысл выражения легко интерпретировать, если переписать его в следующем виде:

. (7.21) Это – энергия, излученная в единичном интервале частот единичным потоком электронов, взаимодействующим с одним ионом. Выражение (7.20) справедливо, как это следует из его вывода, для u << u_max (см. (7.3)), т.е. для частот . (7.22) На практике приближение Крамерса оказывается справедливым для преобладающей части спектра тормозного излучения. Более того выражение (7.20) можно использовать для правильного описания всего спектра, если ввести поправочный функциональный множитель g(w), называемый гаунд - фактором. В пределе малых частот (почти прямолинейные пролеты), когда , гаунд-фактор, например, представляется выражением

. (7.23)

Таким образом, введя в выражение (7.20) гаунд-фактор и интегрируя dk(w) / dw по распределению электронов по скоростям, получим выражение

, (7.24) описывающее спектральную плотность мощности тормозного излучения плазмы. В случае максвелловского распределения по скоростям, интегрируя по спектру, получим практическую формулу для определения полных потерь на тормозное излучение электронов на ионах:

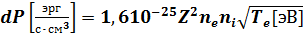. (7.25)

Обратный процесс, называется тормозным поглощением, является трехчастичным и заключается в уменьшении энергии фотона, пролетающего в поле заряженной частицы, с передачей энергии свободному электрону, находящемуся в сфере взаимодействия.

Дата добавления: 2014-01-03