Линейчатое излучение. Вероятность перехода. Сила осциллятора

Вероятность перехода между дискретными уровнями k и m атомной системы (коэффициент Эйнштейна для спонтанного излучения) равна

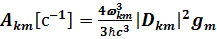, (7.45) где g_m – статвес конечного состояния, D_km – матричный элемент дипольного момента атомной системы

,

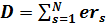а вектор r_s определяет положение s -го электрона атома относительно ядра. Частота излучения, испускаемого или поглощаемого при переходе между этими уровнями, равна

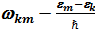. (7.46) Величина времени жизни уровня k по отношению к радиационному распаду находится из выражения

.

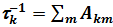Введем форму спектральной линии F_w для излучательного перехода k ® m с нормировкой ò F_wdw = 1. В отсутствии внешних возмущений ее ширина Dw в соответствии с принципом неопределенности пропорциональна 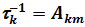. Эта ширина, называется естественной шириной линии, для разрешенных (диполь-дипольных) переходов равна по порядку величины Dw ~ 10⁸ с^-1, что гораздо меньше характерной частоты перехода в оптическом диапазоне w₀ ~ 10¹⁵ с^-1. Как известно, в случае радиационного затухания линия имеет лоренцовский контур

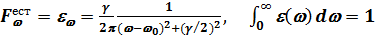, (7.47) где 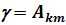- постоянная затухания.

При поглощении фотона с частотой, близкой к частоте перехода w_km, сечение поглощения (в классическом приближении соответствующее вынужденным колебаниям упруго связанного электрона в поле электромагнитной волны E = E₀ sinwt) имеет вид

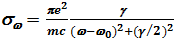, (7.48) где g в случае естественного уширения (7.48) также равна A_km. Сечение поглощения в центре линии при этом равно

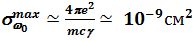. Это сечение (» l²) на семь порядков величины больше характерного газокинетического сечения столкновений атомов pа².

Если атом взаимодействует с окружающей средой (например, испытывает столкновения с другими атомами), то это может приводить к безызлучательному переходу атома в нижние состояния. Это явление в спектроскопии называется тушением возбужденных состояний. Форма спектральной линии в этом случае остается лоренцовской, но величина сечения в максимуме падает, а ширина спектральной линии g возрастает. Тем не менее, в классическом приближении площадь под спектральной линией осциллятора сохраняется даже при наличии столкновений. В расчете на один осциллятор, в соответствии с общепринятыми обозначениями, она равна

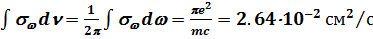. (7.49) Действительно, при резонансном возбуждении осциллятора (w = w₀) амплитуда его колебаний растет пропорционально времени от предыдущего столкновения r_a (t) ~ t. Между столкновениями набирается энергия 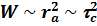, которая при следующем столкновении переходит в тепловую. Тогда энергия, отбираемая от поля в единицу времени

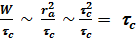, (7.50) пропорциональна времени между столкновениями. В свою очередь, площадь классического осциллятора можно оценить как

.

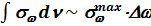Поскольку 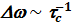, а s_w пропорциональна (W / t_c), то окончательно получаем

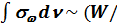t_c .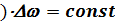

Механизмы уширения линий мы рассмотрим в следующем разделе, а сейчас получим полезные соотношения, описывающие вероятность переходов для линий с некоторым реальным сечением s_w, которое не обязательно удовлетворяет соотношению (7.49). Энергия, поглощаемая на данном переходе в 1 см³ за 1 с, независимо от характера уширения линии равна

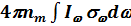, где 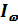[эрг/с×см²с^-1] – “интенсивность” излучения, а S = I_w (W) dwdW - физически измеримая величина, называемая плотностью потока энергии. Если 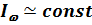в пределах линии, то ее можно вынести из-под интеграла и площадь линии служит мерой поглощательной способности вещества в линии.

Используя принцип детального равновесия, соотношения для термодинамически равновесного излучения и распределение Больцмана для заселенностей уровней, получаем

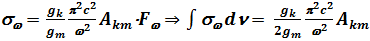. (7.51) Пронормировав выражение (7.51) на площадь классического осциллятора (7.49), получим величину, называемую силой осциллятора, которая для поглощения считается положительной

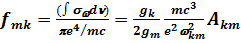. (7.52) Сила осциллятора представляет собой число воображаемых классических осцилляторов, которое обеспечило бы точно такое же поглощение, как и реальная линия. Силы осцилляторов для поглощения и излучения связаны между собой соотношением

– g_k f_km = g_m f_mk.

Величина f_km подчиняется правилу сумм

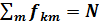, где N – полное число электронов в атомной системе, причем суммирование ведется по всем состояниям дискретного и непрерывного спектров. Силы осцилляторов практически всех линий протабулированы. Для примера некоторые из них приведены в таблице 7.1.

Таблица 7.1. Силы осцилляторов некоторых переходов

Элемент	H	H	N	He	Na	Hg
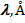переход f	6563(Ha) 2s – 2p 0,416	2p – 3s 0,014	2p – 3d 0,695	2p^3P^0 – 3d^3D 0,62	3s – 3p 0,98	6s6p – 6s7s 0,08

Вероятность перехода можно теперь записать в виде

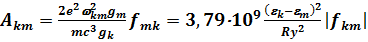. (7.53) Для водородоподобных атомов f_km описывается квазиклассической формулой Крамерса, погрешность которой составляет ~ 30% при всех k и m:

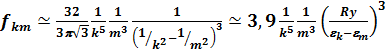. (7.54) Подставив (7.54) в (7.53) и учитывая множитель Z⁴, получим для водородоподобных атомов

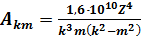. (7.55) Для k = 2, m = 1, Z = 1 получим

A₂₁ = 5×10⁸ с^-1.

Согласно табличным данным A₂₁ = 6,26×10⁸ с^-1 (g₂ / g₁ = 6/2). Видно, что совпадение теории и эксперимента достаточно хорошее для оценок. Для переходов на нижние уровни (m << k)

.

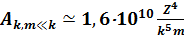Вероятность максимальна при переходе в основное состояние (m = 1). Для перехода на соседнее нижнее состояние вероятность в два раза меньше

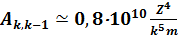. (7.56)

Экстремальное значение A_k найдем, приравняв нулю производную по m знаменателя формулы (7.55):

[ k³m (k² – m²)]^¢ = k³ (k² – 3m²) = 0. (7.57) Поскольку вторая производная – 6k³m < 0, при 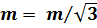величина A_km принимает минимальное значение

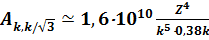. (7.58)

Суммарную вероятность радиационного распада уровня k можно оценить как

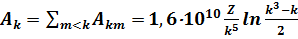. (7.59)

Приведенные выше выражения для A_km и f_km можно использовать и для неводородоподобных атомов, если использовать в них эффективные квантовые числа

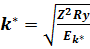, (7.60) где 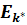- реальная энергия связи данного уровня многоэлектронного атома.

Легко видеть, что верхние (ридберговские ¹) состояния атомов имеют очень большое время жизни по сравнению с нижними (~ k^-5). Поскольку и энергия связи их сопоставима с температурой газа, то заселенность верхних уровней в значительной мере определяется столкновениями. С ростом плотности вероятность столкновительных переходов начинает превышать вероятность испускания фотона для все более глубоких уровней.

______________________________________________________

¹ Ридберговские состояния – высоковозбужденные состояния с большими главными квантовыми числами. Благодаря удаленности от атомного остатка, эти состояния являются с высокой точностью водородоподобными. Энергетический интервал между уровнями уменьшается по мере приближения к границе ионизации.

Дата добавления: 2014-01-03