Лекция № 4

Тема: Основные правила комбинаторики

Основные вопросы, рассматриваемые на лекции:

1. Главные задачи комбинаторики.

2. Правило суммы и правило произведения.

3. Формула включений и исключений для двух множеств.

4. Формула включений и исключений трех множеств.

Краткое содержание лекционного материала

1. Главные задачи комбинаторики. Термин «комбинаторика» был введен Лейбницем («Рассуждения о комбинаторном искусстве», 1666 год).

a) Перечислительной задача. найти число комбинаторных конфигураций с заданными свойствами.

b) Существует ли комбинаторная конфигурация с (очень сложными) заданными свойствами?

c) Алгоритмическая задача. Найти метод генерации комбинаторных конфигураций с заданными свойствами.

d) Оптимизационная задача. Найти комбинаторную конфигурацию с экстремальным значением некоторого параметра.

2. Правило суммы и правило произведения. В теории множеств доказываются следующие правила о числе элементов множеств:

(I) Правило суммы. .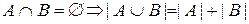

(II) Правило произведения. .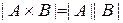

Правило суммы может быть обобщено: если множества попарно не пересекаются, то

.

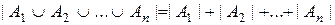Правило произведения может быть обобщено:

.

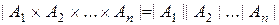Замечание. Операции объединения, пересечения и декартового произведения двух множеств могут быть обобщены на множеств , , …, .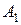

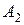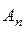Объединение множеств 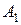, , 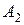…, 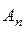содержит те, и только те, элементы, которые принадлежат хотя бы одному из множеств A ₁,…, A_n:

.

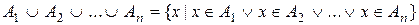Пересечение множеств 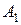, , 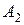…, 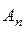содержит те, и только те, элементы, которые принадлежат одновременно каждому из множеств A ₁,…, A_n:

.

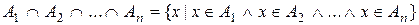Декартово произведение n множеств 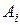, , 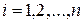содержит последовательности из n элементов, i -й элемент которой принадлежит множеству :

.

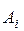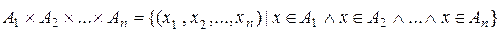Формулировка правила суммы на языке комбинаторики:

(I) Если объект 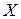можно выбрать 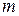способами и объект 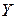можно выбрать способами, причем, ни один из выборов 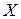не совпадает ни с каким выбором 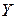, то выбор «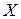или 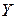» можно осуществить способами.

Формулировка правила произведения на языке комбинаторики:

(II) Если объект X можно выбрать m способами и объект Y можно выбрать способами, то упорядоченную пару (X, Y) можно выбрать mn способами.

Сформулируем правила суммы и произведения в самом общем виде.

Предположим, что смысл выбора объекта Y в том, чтобы выбрать объекты X ₁, X ₂, …, X_k соответственно n ₁, n ₂, …, n_k способами.

(Обобщенное) правило суммы на языке комбинаторики: если для любых i, j Î{1,2,…, k }, i ¹ j, ни один из выборов 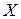_i не совпадает ни с каким выбором 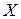_j, то объект Y можно выбрать n ₁+ n ₂+…+ n_k способами.

(Обобщенное) правило произведения на языке комбинаторики: если для любых i Î{1,2,…, k } объект X_i выбирается способами, независимыми от выбора объектов X ₁, …, X_{i -1}, X_{i +1}, …, X_k, то объект Y можно выбрать n ₁ n ₂… n_k способами.

3. Формула включений и исключений для двух множеств. По правилу суммы можно найти число элементов объединения двух непересекающихся множеств. Найти число элементов объединения двух пересекающихся множеств можно по формуле, сформулированной в следующей теореме.

Теорема 1. | A È B |=| A |+| B |-| A Ç B |.

Доказательство. Так как множества A 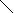B и B, а также A 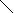B и A Ç B не пересекаются, (A 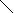B)È B = A È B, (A 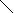B)È(A Ç B)= A, то по правилу суммы

| A È B |=| A 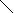B |+| B |,

| A |=| A 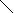B |+| A Ç B |.

Из первого равенства по частям вычтем второе, получим

| A È B |-| A |=| B |-| A Ç B |.

Задача 1. В группе 25 студентов. Из них 16 учат английский, 12 – немецкий, 5 – английский и немецкий. Сколько человек в группе освобождены от изучения английского и немецкого языков?

Решение. Пусть A и B – множества студентов, изучающих соответственно английский и немецкий. Тогда A Ç B – множество студентов, изучающих оба языка, A È B – множество человек в группе, изучающих хотя бы один из двух языков. В силу теоремы 1, | A È B |=| A |+| B |-| A Ç B |=16+12-5=23. Число студентов, освобожденных от изучения языков: 25-23=2.

4. Формула включений и исключений для трех множеств. Метод включений и исключений при подсчете числа элементов объединения трех множеств заключается в следующем: 1) подсчитываем элементы всех трех множеств без различения элементов; 2) вычитываем число элементов, повторяющихся в каких-либо двух списках; 3) прибавляем число элементов, которые повторяются в трех множествах, поскольку они два раза вычитывались.

Теорема 2. | A È B È C |=| A |+| B |+| C |-| A Ç B |-| A Ç C |-| B Ç C |+| A Ç B Ç C |.

Доказательство. Так как A È B È C =(A È B)È C, то, в силу теоремы 1,

| A È B È C |=| A È B |+| C |-|(A È B)Ç C |.

Используем свойство дистрибутивности пересечения относительно объединения: (A È B)Ç C =(A Ç C)È(B Ç C). И ещё раз применим теорему 1:

|(A Ç C)È(B Ç C)|=| A Ç C |+| B Ç C |-|(A Ç C)Ç(B Ç C)|.

По свойствам пересечения, (A Ç C)Ç(B Ç C)= A Ç B Ç C.

Задача 2. Найти число натуральных чисел, не превосходящих 1000 и не делящихся на 3, 5 и 7.

Решение. Пусть A, B и C – множества чисел, не превосходящих 1000 и кратных 3, 5 и 7 соответственно. Тогда A Ç B, A Ç C, B Ç C и A Ç B Ç C – множества чисел, не превосходящих 1000 и кратных 15, 21, 35 и 105 соответственно. Напомним обозначение: [a] – целая часть числа a. Вычислим:

| A |=[1000/3]=333, | B |=[1000/5]=200, | C |=[1000/5]=142,

| A Ç B |=[1000/15]=66, | A Ç C |=[1000/21]=47, | B Ç C |=[1000/35]=28,

| A Ç B Ç C |=[1000/105]=9.

Далее, A È B È C – множество чисел, не превосходящих 1000 и кратных хотя бы одному из чисел 3, 5 и 7. По теореме 2,

| A È B È C |=333+200+142-66-47-28+9=543.

Значит, число натуральных чисел, не превосходящих 1000 и не делящихся ни на одно из чисел 3, 5 и 7, равно 1000-543=457.

В теоремах 1 и 2 доказаны формулы включений и исключений соответственно для двух и трех множеств.

Сформулируем формулу включений и исключений для n множеств:

| A ₁È…È A_n |=| A ₁|+…+| A_n |-| A ₁Ç A ₂|-| A ₁Ç A ₃|-…-| A_{n -1}Ç A_n |+

+| A ₁Ç A ₂Ç A ₃|+| A ₁Ç A ₂Ç A ₄|+…+| A_{n -2}Ç A_{n -1}Ç A_n |+…

…+(-1) ^{n -1}| A ₁Ç A ₂Ç…Ç A_{n -1}Ç A_n |.

Дата добавления: 2014-01-03