Лекция № 5. Тема: Формулы Числа выборок из по

Тема: Формулы Числа выборок из по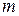

Основные вопросы, рассматриваемые на лекции:

1. Формула числа размещений с повторениями.

2. Формулы числа размещений без повторений. Перестановки.

3. Формулы числа сочетаний без повторений.

4. Формула числа сочетаний с повторениями

Краткое содержание лекционного материала

1. Формула числа размещенийс повторениями. Число всех размещений с повторениями по m из n элементов обозначается .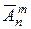

Буква A от французского «arrangement» («приведение в порядок»).

Теорема 1. .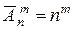

Доказательство. В размещении (x ₁,…, x_m) с повторениями первый элемент x ₁ можно выбрать n способами, второй элемент x ₂ можно выбрать n способами, …, m -й элемент x_m можно выбрать n способами.

По правилу произведения .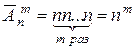

Задача 1. Сколько пятизначных чисел можно составить из всех цифр, кроме 8 и 9?

Решение. 1-й способ. Из числа всех пятибуквенных слов из 8 цифр вычтем число тех слов, которые начинаются с нуля: .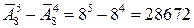

2-й способ. На первое место имеется 7 способов выбора, на последующие места по 8 способов выбора. По правилу произведения 7×8×8×8×8=28672.

2. Формулы числа размещенийбез повторений. Число всех размещений без повторений по m из n элементов обозначается .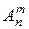

Теорема 2. .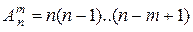

Доказательство. В размещении (x ₁,…, x_m) без повторений первый элемент x ₁ можно выбрать n способами, второй элемент x ₂ можно выбрать n -1 способами, …, m -й элемент x_m можно выбрать n -(m -1)= n - m +1 способами.

n - факториал – это произведение первых n положительных целых чисел: n!=1×2×3×…× n. Считается, что 0-факториал равен 1: 0!=1.

Теорема 3. .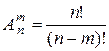

Доказательство. Правую часть равенства теоремы 2 умножим и разделим на произведение (n - m)×(n - m -1)×…×2×1=(n - m)!

Задача 2. Сколько пятизначных чисел с разными цифрами можно составить из всех цифр, кроме 8 и 9?

Решение. 1-й способ. .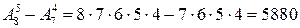

2-й способ. На первое место имеется 7 способов выбора, на второе – тоже 7 способов (прибавляется 0), на третье – 6 способов, на четвертое – 5 способов, на пятое – 4 способа. По правилу произведения 7×8×8×8×8=28672.

Перестановка из n элементов – это размещение без повторений из n элементов по n. Число всех перестановок из элементов обозначается P_n.

Буква P от французского «permutation» («перестановка»).

Из теоремы 2 или теоремы 3 следует, что P_n = n!

3. Формулы числа сочетаний без повторений. Число всех сочетаний без повторений по m из n элементов обозначается .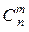

Буква C от французского «combinaison» («сочетание»).

Теорема 4. .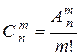

Доказательство. Каждое размещение без повторений (x ₁,…, x_m) по m из n можно построить в 2 шага: вначале строится сочетание без повторений { x ₁,…, x_m } по m из n, а затем – перестановка (x ₁,…, x_m) из m элементов множества { x ₁,…, x_m }. По правилу произведения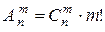

Теорема 5. .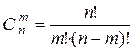

Доказательство. Следствие теорем 4 и 3.

Теорема 6. .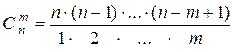

Доказательство. Следствие теорем 4 и 2.

Формула теоремы 5 используется при доказательствах свойств 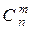, а формула теоремы 6 – при вычислениях значений 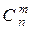для небольших n.

Решение. Игрок может выбрать 7 костей из 28 костей 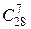способами.

Задача 3. В корзине 14 груш и 25 яблок. Сколькими способами можно выбрать из корзины 4 груши и 5 яблок?

Решение. 4 груши из 14 можно выбрать 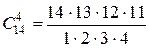способами, а 5 яблок из 25 – 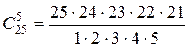способами. Независимо от выбора 4-х груш, каждый раз выбирается 5 яблок. Поэтому применим правило произведения, и получим искомое число: .

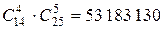4. Формулы числа сочетаний с повторениями. Число всех сочетаний с повторениями по m из n элементов обозначается .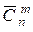

Формула числа сочетаний с повторениями из n элементов по m сводится к формуле числа сочетаний без повторений из n + m -1 элементов по m.

Теорема 7. .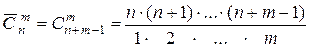

Доказательство. Сочетание a₁a₂…a _m не меняется от перестановки элементов. Поэтому мы одинаковые элементы можем размещать рядом.

Пусть a₁, a₂, …, a _m Î{ a ₁, a ₂, …, a_n }. Тогда каждое сочетание по m из n элементов множества { a ₁, a ₂, …, a_n } с повторениями можно представить следующим образом:

a ₁… a ₁(s ₁ раз) a ₂… a ₂(s ₂ раз)… a_n … a_n (s_n раз), (1)

где s ₁, s ₂,…, s_n ³0, s ₁+ s ₂+…+ s_n = m.

Каждому сочетанию (1) мы поставим в соответствие последовательность

1…1(s ₁ раз)01…1(s ₂ раз)0…01…1(s_n раз). (2)

В последовательности (2) m единиц и n -1 нулей. Указанное соответствие является биекцией между множеством всем сочетаний с повторениями по m из n элементов множества { a ₁, a ₂, …, a_n } и множеством всех последовательностей, состоящих из единиц и n -1 нулей.

Рассмотрим (m + n -1)-множество A номеров элементов последовательности (2). Множество номеров элементов последовательности (2), равных единице, является m -подмножеством множества A, т.е. сочетанием без повторений по m из m + n -1 элементов множества A. Это соответствие между множеством всех последовательностей вида (2) и множеством всех m -подмножеством множества A является биекцией. Значит, сочетаний с повторениями по m из n столько же, сколько сочетаний без повторений по m из m + n -1.

Задача 4. В буфете продаются 5 сортов пирожков: с яблоками, с капустой, с картошкой, с мясом и с грибами (цена всех пирожков одинакова). Сколькими способами можно сделать покупку из 10 пирожков?

Решение. Мы имеем дело с сочетаниями из 5 элементов множества сортов пирожков, с повторениями, по 10 элементов. Применим формулу теоремы 7 при , : .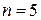

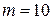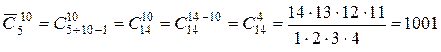Дата добавления: 2014-01-03