Перестановки с повторениями

Перестановкой с повторениями называется размещение с повторениями по n из n элементов k -множества M (k £ n) со следующим дополнительным условием: различные k элементов множества M повторяются соответственно n ₁,…, n_k раз, 1£ n ₁,…, n_k £ n, n ₁+…+ n_k = n.

Теорема 6. Число перестановок с повторениями различных k элементов n ₁,…, n_k раз, 1£ n ₁,…, n_k £ n, n ₁+…+ n_k = n, равно .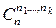

Доказательство. Пусть M – множество номеров перестановки с повторениями, одной из указанных в условии теоремы, M ₁,…, M_k – множества номеров с одинаковыми элементами, повторяющимися n ₁,…, n_k раз соответственно. Тогда семейство множеств { M ₁,…, M_k } будет разбиением множества M на k блоков. Значит, каждой перестановке с повторениями соответствует вполне определенное разбиение множества M на k блоков. Ясно, что это соответствие является биекцией. Значит, искомое число перестановок с повторениями равно числу разбиений на k блоков .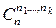

Задача 3. Найти число всех перестановок букв слова «баобаб».

Решение. n ₁=3 (буква «б»), n ₂=2 («а»), n ₁=1 («о»), значит, .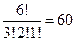

3. Производящие функции. Формальный ряд a ₀+ a ₁ x + a ₂ x ²+…+ a_kx^k +… называется производящей функцией последовательности a ₀, a ₁, a ₂,…, a_k,…

Производящая функция является или сходящимся рядом, или расходящимся рядом. Два расходящихся ряда могут быть равны как функции, но быть производящимися функциями различных последовательностей. Например, ряды 1+2 x +2² x ²+…+2 ^kx^k +… и 1+3 x +3² x ²+…+3 ^kx^k +… определяют одну и ту же функцию (равную 1 в точке x =1, неопределенную в точках x >1), но являются производящими функциями различных последовательностей.

Свойства производящих функций последовательностей:

сумма (разность) производящих функций последовательностей a_n и b_n равна производящей функции сумме (разности) последовательностей a_n + b_n;

произведение производящих функций последовательностей a_n и b_n является производящей функцией свёртки последовательностей a_n и b_n:

c_n = a ₀ b_n + a ₁ b_{n -1}+…+ a_{n -1} b ₁+ a_nb _0.

Пример 1. Функция 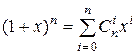является производящей для последовательности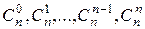

Пример 2. Функция 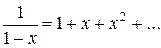является производящей для последовательности 1, 1, 1, …

Дата добавления: 2014-01-03