Модели массового обслуживания

В теории массового обслуживания изучаются системы, на вход которых поступает случайный поток заявок (требований), приходящихся в общем случае на случайные моменты времени. Поступившая заявка обслуживается в системе путем предоставления ей некоторых ресурсов на какое-то время и, будучи в той или иной мере обслуженной, покидает систему.

Помимо случайного появления заявок на обслуживание и случайной длительность обслуживания каждой заявки для систем массового обслуживания характерным является наличие очередей, в которых заявки ждут момента освобождения ресурсов, занятых обслуживанием других заявок.

Поскольку события, происходящие в ВС, носят случайный характер, то для их изучения наиболее подходящими являются вероятностные математические модели теории массового обслуживания. Так, используемые в настоящее время в локальных сетях протоколы канального уровня используют методы доступа к среде, основанные на ее совместном использовании несколькими узлами за счет разделения во времени. В этом случае, как и во всех случаях разделения ресурсов со случайным потоком запросов, могут возникать очереди.

Объектами исследования в теории массового обслуживания являются системы и сети массового обслуживания (СМО). В системах, моделируемых в виде СМО, различают статические и динамические объекты. Статические объекты – обслуживающие аппараты (ОА) или ресурсы, моделируют средства обработки информации (аппаратные и программные). Динамические объекты – заявки (запросы, требования) моделируют решаемые в ВС задачи. Поток заявок физически представляет собой явления одной природы, например попытки модемного соединения, запросы к базе данных и т. д. С математической точки зрения поток заявок на обслуживание характеризуется законом распределения случайной величины – времени между появлением соседних заявок.

Функционирование СМО представляется как процесс прохождения заявок через систему. Правило, по которому заявки поступают из очередей на обслуживание в ОА, называется дисциплиной обслуживания, а величина преимущественного права на обслуживания – приоритетом. Для каждого приоритета на входе ОА образуется своя очередь. Если заявка поступает на вход ОА, занятого обслуживанием заявки с более низким приоритетом, то возможно прерывание ранее начатого обслуживания – такой приоритет называется абсолютным. Если прерывания ранее начатого обслуживания не происходит – приоритет относительный.

СМО бывают одно- и многоканальными в зависимости от числа ОА, параллельно обрабатывающих входной поток заявок; одно- и многофазными в зависимости от числа последовательно включенных ОА.

Классификационное обозначение СМО имеет вид A/B/C/D/E, где позиции, обозначенные буквами, означают следующие характеристики:

A – обозначение закона распределения времени поступления заявок входного потока (обозначение М соответствует экспоненциальному закону распределения, Г – гамма-распределению, Е – распределению Эрланга, Н – гиперэкспоненциальному распределению, N – нормальному распределению, R – равномерному распределению, D – постоянному времени обслуживания, G – произвольному или неизвестному закону распределения, Gr – групповому (пакетному) поступлению заявок на обслуживание);

B – обозначение закона распределения времени обслуживания в устройствах (используются те же обозначения, что и для распределения времени поступления заявок);

C – число ОА;

D – число мест в очереди (для неограниченных опускается);

E – дисциплина обслуживания: для дисциплины FIFO данное обозначение опускается; также используются обозначения LIFO, RANDOM, SF (Short Forward – «короткие вперед» – в первую очередь обслуживаются те заявки из очереди, которые требуют меньшего времени обслуживания).

Примеры обозначений:

- М/М/1: СМО с одним ОА, бесконечной очередью, экспоненциальными законами распределения интервалов времени между поступлениями заявок и времени обслуживания, дисциплиной обслуживания FIFO;

- Е/Н/m/r/LIFO: СМО с m обслуживающими аппаратами, очередью, ограниченной r местами, эрланговским законом распределения интервалов между поступлениями заявок, гиперэкспоненциальным распределением времени обслуживания в ОА, дисциплиной обслуживания LIFO.

Если СМО в дополнение к перечисленным характеристикам обладает какими-либо особенностями, последние добавляются к обозначению в качестве комментария (например, СМО типа G/G/1 с ненадежным ОА и временем ожидания в очереди, ограниченным 3,5 секундами).

Для моделирования ВС наиболее часто используются комбинации типов СМО, приведенные в таблице 8.

Таблица 8

Наименование	Обозначение	Графическое обозначение	Описание
Одноканальная СМО с ожиданием	G/G/1		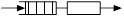Один ОА с бесконечной очередью. С той или иной долей приближения моделирует любой узел или процесс ВС, например механизм разделения среды протокола Ethernet.
Одноканальная СМО с потерями	G/G/1/r		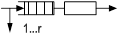Один ОА с конечным числом мест в очереди. Если число заявок превышает число мест в очереди, то лишние заявки теряются. Используется при моделировании каналов передачи в ВС.
Многоканальная СМО с ожиданием	G/G/m		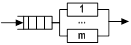Несколько параллельно работающих ОА с общей бесконечной очередью. Используется при моделировании групп абонентских терминалов ВС, работающих в диалоговом режиме.
Многоканальная СМО с потерями	G/G/m/r		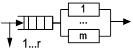Несколько параллельно работающих ОА с общей очередью, число мест в которой ограничено. Используются для моделирования каналов связи в ВС.
Одноканальная СМО с групповым поступлением заявок	Gr/G/1		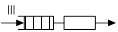Один ОА с бесконечной очередью. Перед обслуживанием заявки группируются в пакеты по определенному правилу. Используется для моделирования узлов коммутации.
Одноканальная СМО с групповым обслуживанием заявок	G/Gr/1		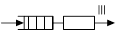Один ОА с бесконечной очередью. Заявки обслуживаются пакетами, составляемыми по определенному правилу. Используется для моделирования узлов коммутации.

Целью моделирования СМО является определение статистических и операционных характеристик, определяющих поведение систем в процессе функционирования. Вероятность потери заявки (вероятность отказа) одна из основных статистических характеристик СМО. Помимо этого по результатам функционирования СМО определяют следующие характеристики: средняя длина очереди, коэффициент загрузки ОА (доля времени, в течение которого ОА занят обслуживанием), среднее время ожидания заявки в очередях СМО, среднее время обслуживания заявки в ОА СМО, среднее время пребывания заявки в СМО и т. д.

К основным операционным характеристикам относятся:

Q(t) – длина очереди в момент времени t, т. е. число заявок, ожидающих обслуживания с учетом или без тех заявок, обслуживание которых уже началось;

Q_n – длина очереди на n –й стадии, при этом предполагается, что стадии реализуются в дискретном режиме и определяются теми или иными событиями (например, появлением запроса на обслуживание, или выбытием заявки из системы);

W(t) – виртуальная продолжительность ожидания относительно момента времени t, т. е. время ожидания обслуживания для заявки, которое поступит в систему в момент времени t;

W_n – продолжительность периода, в течение которого n -я заявка ожидает обслуживания;

T_i – продолжительность периода занятости системы, начало которого соответствует Q(0)=i, т. е. длина периода занятости системы, начинающегося при наличии в системе i заявок;

I_n – продолжительность n –го периода простоя системы, т. е. длина интервала, в течении которого система в n –й раз оказывается незанятой.

Наряду с указанными характеристиками используются их различные модификации – полная продолжительность пребывания запроса в системе, операционный цикл – сумма продолжительности периода занятости и непосредственно следующего за ним периода простоя, суммарное полезное время (доля времени с полной загрузкой), и т. д.

Многие системы массового обслуживания обладают тем свойством, что по истечении определенного времени их поведение в некотором смысле стабилизируется. Формально это выражается в появлении стационарных (периодических) свойств процессов Q(t) и W(t) при t®¥, и Q_n, W_n при n®¥. Условия, при которых системы переходят в стационарное состояние, представляют отдельный интерес для исследования.

В соответствии с общей классификацией моделей различают аналитические и имитационные модели СМО.

Дата добавления: 2014-01-03