Закон Пуассона

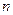Рассмотрим асимптотическое приближение биномиального закона, когда велико, а 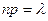конечно (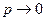). В этом случае формулу (2.12.1) можно преобразовать следующим образом:

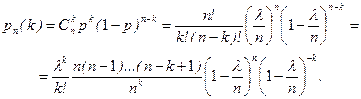
Переходя к пределу при 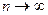и учитывая, что

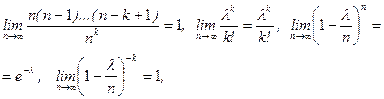
получим

.

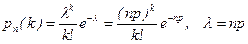Данное распределение принято называть распределением Пуассона. Законом распределения Пуассона называется распределение вероятностей дискретной сл.в. К, принимающей значения 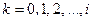с вероятностями

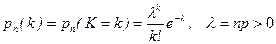. (2.13.1)

Графики распределения Пуассона при различных значениях параметра 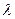приведены на рис.2.23.

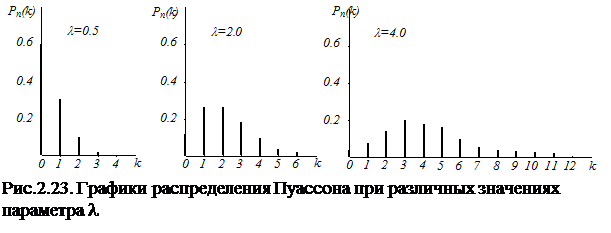
Основные свойства распределения Пуассона.

1. Для закона Пуассона справедливо рекуррентное соотношение

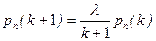, (2.13.2)

которое можно использовать для расчета последовательных членов ряда (1).

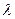2. Распределение зависит от одного параметра , имеющего смысл математического ожидания сл.в. К.

3. Для закона Пуассона характерно равенство м.о. и дисперсии:

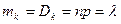. (2.13.3)

Этим свойством часто пользуются на практике для проверки гипотезы о том, что сл.в. распределена по закону Пуассона.

4. Распределение несимметрично. С ростом параметра 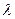значения вероятностей ряда убывают и распределение становится все более симметричным.

5. Распределение Пуассона устойчиво относительно линейных операций над сл.в. Это означает, что если имеется n попарно независимых случайных величин 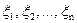, распределенных по закону Пуассона с м.о. 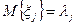для 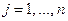, то их линейная сумма

,

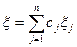где 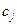- целые числа, также подчиняются закону Пуассона с параметром .

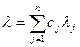В статистике закон Пуассона часто называют законом редких явлений за его свойство выражать биномиальное распределение при большом " n " и малой вероятности " p ".

Во многих задачах закон Пуассона выступает не как асимптотическое приближение биномиального, а в качестве совершенно точного. Так, например, обстоит дело применительно к точечным процессам или потокам (§7.6).

Случайным потоком называется последовательность событий, происходящих друг за другом в случайные моменты времени 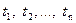(поступление сообщений по каналу связи, моменты отказов в сложной РЭС, заявки на обслуживание, вызовы на телефонную станцию и т.д.).

Графически поток событий можно иллюстрировать множеством точек, расположенных на оси времени (рис.2.24).

Случайный поток называется простейшим (пуассоновским), если он обладает свойствами стационарности, отсутствием последействия и ординарности.

Стационарность потока означает, что вероятность наступления некоторого числа событий в течение заданного отрезка времени 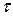не зависит от расположения этого отрезка на оси времени, а зависит только от величины отрезка.

Отсутствие последействия характеризуется тем, что отдельные события в потоке происходят независимо друг от друга, т.е. для любых непересекающихся интервалов времени число событий в одном из них не зависит от числа событий в другом.

Свойство ординарности означает, что вероятность появления двух и более событий на достаточно малом интервале времени 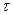(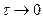) исчезающе мала по сравнению с вероятностью появления одного события, т.е. ординарным считается поток относительно редких явлений.

Если постоянная интенсивность потока 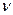известна, то вероятность появления k событий простейшего потока за время длительностью 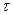определяется формулой Пуассона

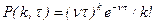, (2.13.4)

где 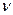- интенсивность потока, т.е. среднее число точек, приходящихся на единичный интервал времени. Это выражение отражает все свойства простейшего потока.

Свойство стационарности проявляется в том, что вероятность появления k событий (точек) за время 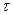, при заданной интенсивности 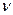, является функцией k и .

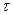Отсутствие последействия характеризуется тем, что формула не использует информации о появлении событий до начала рассматриваемого промежутка.

Свойство ординарности подтверждается тем обстоятельством, что при малых значениях 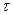вероятность 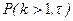появления более одного события пренебрежимо мала по сравнению с вероятностью 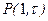наступления одного события.

Формулу (4) называют формулой Пуассона для случая непрерывного времени. Строгий ее вывод будет дан в § 7.6. Для нескольких значений k зависимость (4) представлена на рис.2.25.

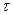Формула (4) позволяет найти: вероятность того, что на интервале окажется от 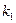до 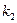точек (событий):

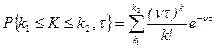; (2.13.5)

вероятность того, что на интервал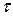не попадет ни одной точки

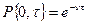; (2.13.6)

вероятность того, что на интервал 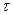попадет одна точка (произойдет одно событие)

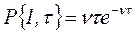. (2.13.7)

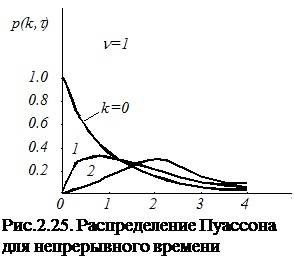Законом распределения Пуассона можно описывать поступление вызовов на телефонную станцию, поступление требования на ремонт или переналадку оборудования, число импульсов хаотической импульсной помехи, дефекты на заданном участке проводной линии связи и т.д.

Пример 2.13.1. Вероятность того, что некоторое изделие будет содержать скрытый дефект, равна 0,002. Найти вероятность того, что таких изделий в партии из 500 штук будет: 1) ровно три; 2) менее трех; 3) более трех; 4) хотя бы одно.

По условию число n =500 велико, вероятность p =0,002 мала, 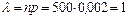, события (наличие скрытого дефекта) независимы. Поэтому следует применить формулу Пуассона (1)

:

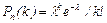1) ;

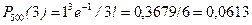2) ;

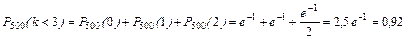3)

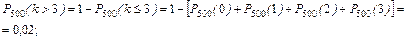
4) .

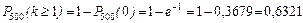Пример 2.13.2. Среднее число вызовов, поступающих на АТС в одну минуту, равно трем. Требуется определить вероятность того, что за 2 мин поступит: 1) четыре вызова; 2) менее четырех вызовов; 3) не менее четырех вызовов.

По условию, 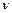=3, 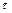=2. Воспользовавшись формулой (4), получим

;

;

.

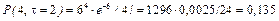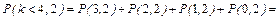
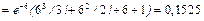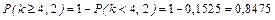Дата добавления: 2014-01-03