Биномиальный закон распределения вероятностей

Дискретная сл.в. называется распределенной по биномиальному закону, если она может принимать только целые неотрицательные значения с вероятностями

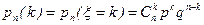, (2.12.1)

где 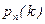- вероятность появления события k раз при n испытаниях, k =0,1,..., n - текущая переменная, n и p - параметры биномиального распределения: n - число проведенных испытаний, p - вероятность "успеха", а q =1- p - вероятность "неуспеха" в каждом испытании.

Равенство (1) называется формулой Бернулли, а распределение вероятностей, задаваемое функцией 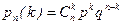- биномиальным распределением или распределением Бернулли. Такое распределение описывает закономерности в одной из важнейших схем теории вероятностей - схеме Бернулли, когда проводятся повторные независимые испытания, причем в каждом из них имеется только два возможных исхода, вероятности которых не меняются от испытания к испытанию.

"Классической" схемой (моделью) Бернулли является подбрасывание симметричной монеты n раз (или n симметричных монет одновременно). К схеме Бернулли также относятся наблюдения за исправной работой идентичных приборов, для которых вероятности безотказной работы в течение времени Т одинаковы.

Биномиальным распределение называется потому, что имеет такой же вид, как и коэффициент разложения бинома Ньютона в ряд по степеням x:

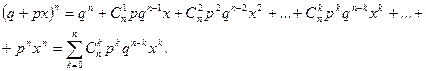При x =1 получим условие нормировки распределения: .

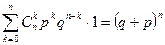Функция (p+qx) называется производящей. С ее помощью можно обобщить формулу Бернулли на случай серии независимых испытаний, проводимых в переменных условиях, когда в i -ом испытании вероятность появления события равна 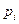, а вероятность противоположного события 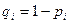. В этом случае вероятность 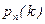находится как коэффициент при 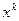в разложении

.

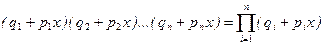Пример 2.12.1. Пусть требуется определить вероятность 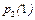того, что при двух испытаниях событие А появится один раз, если вероятность этого события в первом испытании равна 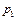, а во втором - .

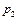В данном случае

.

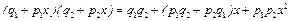Следовательно, .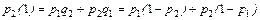

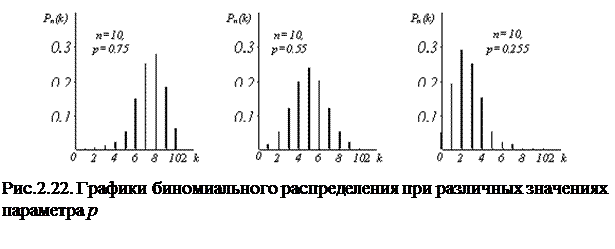
Биномиальное распределение при различных значениях параметров n и p показано на рис.2.22.

Приведем основные свойства биномиального распределения.

1. Распределение определяется двумя параметрами: числом испытаний n и вероятностью p отдельного испытания.

2. Математическое ожидание 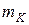равно:

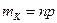. (2.12.2)

Для доказательства представим случайную величину K (общее число успехов) в виде суммы успехов (появлений событий А) в отдельных испытаниях

,

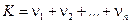где 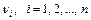, - случайные величины, принимающие два значения:

1 - с вероятностью 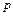и 0 с вероятностью :

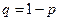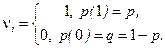
По определению, .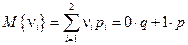

Используя свойства м.о., получим

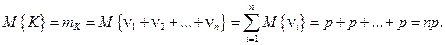
3. Дисперсия 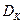сл.в. K определяется формулой

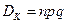. (2.12.3)

Действительно, используя аналогичную методику, будем иметь

.

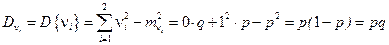Величины 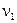, , 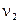…, 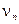взаимно независимы. Поэтому по свойствам дисперсии получим

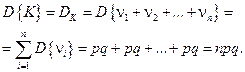
4. Среднее квадратическое отклонение равно

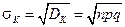. (2.12.4)

Находим отношение 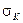к :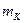

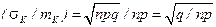. (2.12.5)

Формула (5) показывает, что с увеличением числа испытаний n относительное рассеивание сл.в. K уменьшается, а абсолютное - растет. Этот результат играет важную роль при практических измерениях

5. Максимум вероятности 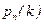достигается при значениях k, удовлетворяющих неравенствам

.

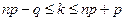Если величина (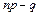) есть целое число, то наибольшее значение 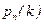достигается при двух значениях k: 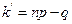и 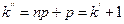. Если же (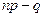) - не целое число, то максимум 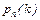будет при том значении k, которое заключено между 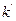и .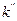

6. При 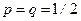, , 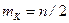, 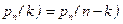т.е. биномиальное распределение симметрично относительно среднего значения (рис. 2.22).

Пример 2.12.2. Найти положение максимума вероятности 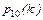, если n =10, а p =0,75. В данном случае 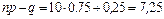т.е. число нецелое. Значит, максимум 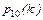будет при таком k, которое заключено между 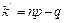=7,25 и 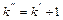=8,25, что подтверждается графиком рис. 2.22.

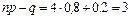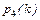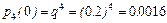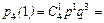
Пусть теперь n =4, p =0,8, q =0,2. В этом случае . Так как получили целое число, то максимум будет при двух значениях аргумента. Покажем это: , , 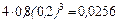, , 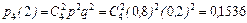, 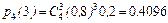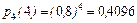т.е. максимум достигается при k =3 и k =4.

Биномиальное распределение применяется в теории надежности, при контроле качества, выборочном обследовании и других областях. С ним связаны такие распределения, как гипергеометрическое, геометрическое, отрицательное биномиальное и распределение Паскаля [5, 24, 30].

Пример 2.12.3. Промышленная продукция определенного вида изготавливается крупными партиями. Из каждой партии случайным образом выбирается 20 изделий. Партия принимается, если выборка содержит не более трех дефектных изделий. Требуется определить вероятность принятия партии (если в процессе производства в среднем 10% изделий получаются дефектными), а также м.о., дисперсию и среднее квадратическое значение сл.в. K - числа дефектных изделий.

По условию имеем n =20, 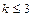, p =0,1, q =1-0,1=0,9. Следовательно,

,

, ,

.

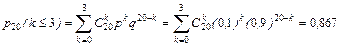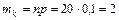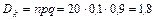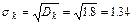Если случайная величина K распределена по биномиальному закону, то при большом n вычисление 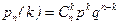становится затруднительным. В подобных случаях целесообразно использовать асимптотические формулы. При этом применяются две такие формулы.

1. Формула Пуассона (закон Пуассона), когда 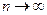, а величина 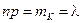остается конечной. Это означает, что 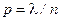мала, т.е. имеет место закон редких явлений, так как ограниченность 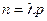при 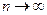означает, что .

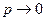2. Формула Лапласа (нормальный закон), которая применяется пр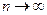и и 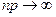, что означает постоянство p, т.е. p =соnst.

Дата добавления: 2014-01-03