Равномерный закон распределения

Непрерывная сл.в. x распределена равномерно, если на интервале [ a, b) ее плотность постоянна, т.е. имеет вид

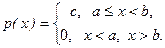
Так как все возможные значения сл.в. x принадлежат интервалу [ a, b), то должно выполняться условие нормировки:

;

.

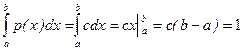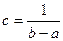Следовательно, аналитическое выражение п.в. при равномерном распределении следует записать в виде

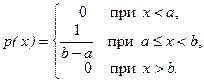(2.15.1)

Функция распределения F(x) определяется путем интегрирования плотности р(х):

.

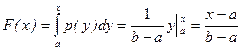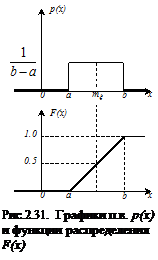
На участке 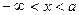функция F(x) =0. F(b) =1 при x=b и далее на участке 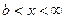остается равной единице. Следовательно,

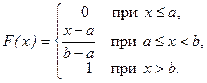(2.15.2)

Вид функций р(х) и F(x) показан на рис. 2.31.

Отметим основные свойства равномерного (прямоугольного) распределения.

1. Математическое ожидание сл.в. x, распределенной по равномерному закону, равно

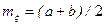. (2.15.3)

Действительно,

.

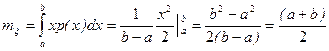2. Дисперсия равномерного распределения определяется формулой

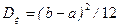. (2.15.4)

В самом деле,

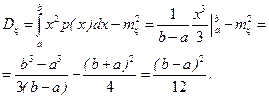
3. Из формул (1…4) видно, что для равномерного распределения задание интервала существования [ a, b) полностью определяет все вероятностные характеристики сл.в. x.

4. Вероятность попадания равномерно распределенной сл.в. x в интервал 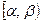равна:

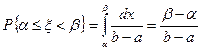. (2.15.5)

Особое значение имеет равномерное распределение на интервале [0, 1), которое является основой для формирования требуемых распределении при статистическом моделировании РЭС. Таким образом,

Современные ЭЦВМ и компьютеры имеют стандартную подпрограмму, предназначенную для воспроизведения сл.в., равномерно распределенных на единичном интервале (датчик случайных чисел).

Равномерное распределение часто применяется в качестве математическом модели для таких реальных явлений как: случайная начальная фаза гармонического колебания, ошибки округления в ЭВМ, ошибки квантования и т.д.

Пример 2.15.1. Разность фаз 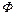двух независимо включаемых генераторов синусоидального напряжения описывается равномерной плотностью вероятности в интервале от - p до p. Требуется: 1) записать выражения для п.в. и функции распределения разности фаз и построить их графики; 2) вычислить м.о. 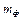, дисперсию 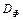и среднее квадратическое значение 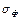сл.в. Ф. Найти вероятность нахождения сл.в. Ф в интервале от p/3 до p/2.

1) Из условия нормировки имеем , .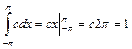

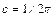Следовательно,

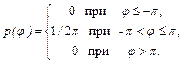
По п.в. находим функцию распределения :

.

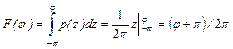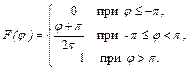
Графики функци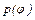й и 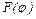приведены соответственно на рис.2.32 и рис.2.33.

2) ;

; .

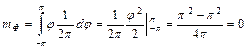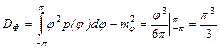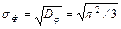3) .

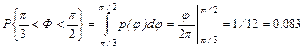Дата добавления: 2014-01-03