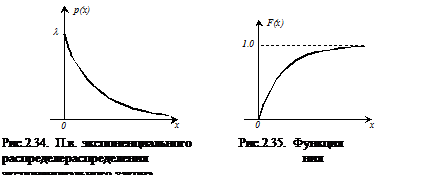
Экспоненциальное распределение. Непрерывная сл.в. имеет экспоненциальный (показательный) закон распределения, если ее п.в

Непрерывная сл.в. имеет экспоненциальный (показательный) закон распределения, если ее п.в. задана выражением

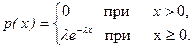(2.16.1)

где l - постоянная положительная величина. По п.в. находим функцию распределения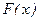

.

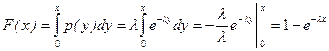Следовательно,

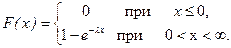(2.16.2)

Графики функци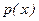й и 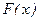представлены соответственно на рис.2.34 и рис.2.35.

Вычислим основные характеристики экспоненциального распределения:

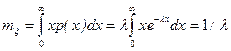; (2.16.3)

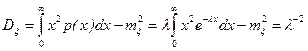. (2.16.4)

Среднее квадратическое отклонение равно

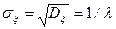. (2.16.5)

Вероятность попадания сл.в. x в заданный отрезок определяется как приращение функции распределения на этом отрезке

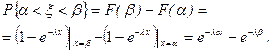(2.16.6)

Экспоненциальное распределение (1) определяется одним параметром l. Задание его полностью определяет все вероятностные характеристики сл.в.

Экспоненциальный закон широко используется в теории надежности, теории систем массового обслуживания и других областях. По экспоненциальному закону, в частности, может быть распределено время безотказной работы РЭС, время между появлениями двух последовательных событий простейшего потока.

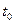Пусть, например, элемент начинает работать в момент времени =0, а по истечении времени длительностью t происходит отказ. Тогда функция распределения 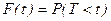, где cл.в. Т -длительность времени безотказной работы элемента, определяет вероятность отказа за время t. Следовательно, вероятность безотказном работы за это же время t, т.е. вероятность противоположного события (Т > t), равна

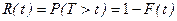. (2.16.7)

Функцию R(t) называют функцией надежности. При экспоненциальном распределении сл.в. Т имеем 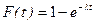. Тогда

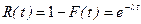, (2.16.8)

где l - интенсивность отказов.

Большой набор п.в. 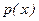дает система кривых Пирсона, задаваемая дифференциальным уравнением

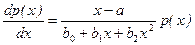. (2.16.9)

В зависимости от значений отдельных параметров в качестве решения уравнения (9) получаются 12 типов кривых, каждая из которых полностью определяется первыми четырьмя моментами сл.в. [12, 15, 24]. Эти кривые часто используются для приближенного представления п.в. сл.в. x подходящим аналитическим выражением, зная некоторые числовые характеристики этой величины.

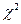Нормальное распределение, гамма-, бэта- и -распределения, распределение Стьюдента и другие удовлетворяют уравнению (9) и, следовательно, являются частными случаями семейства кривых Пирсона.

Пример 2.16.1. Сл.в. Т -время безотказной работы элемента распределено по показательному закону, причем среднее время 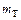безотказной работы равно 400 часов. Определить вероятность того, что элемент проработает без отказа не менее 600 часов.

По условию 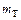=400 часов. Следовательно, .

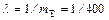Тогда

.

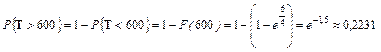Дата добавления: 2014-01-03