Лекция № 18

Тема: алгоритм беллмана–форда

Основные вопросы, рассматриваемые на лекции:

1. Формулировка задачи.

2. О динамическом программировании.

3. Выполнение алгоритма на графе без отрицательных циклов.

Краткое содержание лекционного материала

1. Формулировка задачи. Алгоритм Беллмана – Форда – алгоритм поиска кратчайшего пути во взвешенном графе. За время O (| V |×| E |) алгоритм находит кратчайшие пути от одной вершины графа до всех остальных. В отличие от алгоритма Дейкстры, алгоритм Беллмана – Форда допускает рёбра с отрицательным весом. Длиной пути называется сумма весов рёбер, входящих в этот путь. Надо найти кратчайшие пути от выделенной вершины s до всех вершин графа.

Кратчайших путей может не существовать. Например, в графе, содержащем цикл с отрицательным суммарным весом, существует сколь угодно короткий путь от одной вершины этого цикла до другой.

2. О динамическом программировании. Ричард Беллман в сороковых годах использовал словосочетание «динамическое программирование» для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. Слово «программирование» здесь (также, как в словосочетании «линейное программирование») не имеет отношения к программированию как к написанию кодов.

Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.

1. Разбиение задачи на подзадачи меньшего размера.

2. Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.

3. Использование полученного решения подзадач для конструирования решения исходной задачи.

3. Решение задачи на графе без отрицательных циклов.

Для нахождения кратчайших путей от одной вершины до всех остальных, воспользуемся методом динамического программирования. Построим матрицу A_ij, элементы которой будут обозначать следующее: A_ij – это длина кратчайшего пути из s в i, содержащего не более j рёбер.

Путь, содержащий 0 рёбер, существует только до вершины s. Таким образом, A_{i 0} равно 0 при i = s, и +∞ в противном случае.

Теперь рассмотрим все пути из s в i, содержащие ровно j рёбер. Каждый такой путь есть путь из ребра, к которому добавлено последнее ребро. Если про пути длины все данные уже подсчитаны, то определить j -й столбец матрицы не составляет труда.

Так выглядит алгоритм поиска длин кратчайших путей в графе без отрицательных циклов:

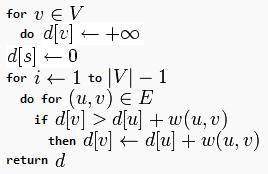
Здесь V — множество вершин графа G, E — множество его рёбер, а w — весовая функция, заданная на ребрах графа (возвращает длину дуги ведущей из вершины v в u), d - массив, содержащий расстояния от вершины s до любой другой вершины.

Дата добавления: 2014-01-03