Лекция № 17

Тема: кратчайшие пути. Алгоритм Дейкстры

Основные вопросы, рассматриваемые на лекции:

1. Задача о кратчайшем пути на графе.

2. Определение алгоритма Дейкстры.

3. Выполнение алгоритма Дейкстры на примере графа.

Краткое содержание лекционного материала

1. Задача о кратчайшем пути на графе. Припишем всем ребрам графа веса – положительные числа. Кратчайший путь от вершины 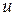до вершины 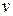– это маршрут от 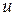до 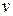с минимальной суммой весов ребер маршрута. Надо найти все кратчайшие пути от данной вершины до всех остальных вершин.

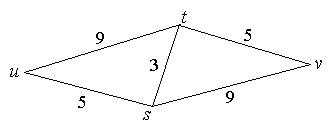
Пример. Маршрут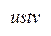имеет сумму весов ребер 13, а маршруты 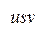и 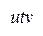– 14. Значит, 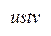– кратчайший путь от 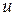до .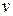

Задача о кратчайшем пути на графе решается алгоритмом, изобретенным нидерландским ученым Э. Дейкстрой в 1959 г.

Расстоянием от 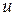до 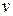называют сумму весов ребер по одному из маршрута от 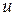до .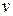

2. Определение алгоритма Дейкстры. Каждой вершине 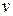ставим метку – минимальное известное расстояние от данной вершины .

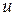Алгоритм работает пошагово – на каждом шаге он «посещает» одну вершину и пытается уменьшить метку вершины. Если все вершины посещены, алгоритм завершается.

Метка вершины 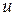равна 0. В начале метки остальных вершин предполагаются равными +¥. Иначе, из ещё не посещённых вершин выбирается вершина 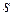, имеющая минимальную метку. Рассматривают всевозможные маршруты с началом 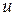, в которых 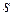является предпоследним пунктом.

Для каждой не посещённой вершины 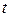, смежной с вершиной 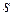, находят сумму значения текущей метки 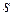и веса ребра, соединяющего 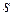и 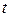. Если полученная сумма s меньше значения t метки 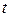, то метку t заменяют меткой s.

Рассмотрев все не посещённые вершины, смежные с вершиной 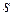, вершина 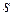отмечается как посещенная, и повторяется шаг алгоритма.

4. Выполнение алгоритма Дейкстры на примере графа. Требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

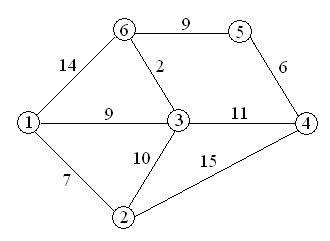
Кружками обозначены вершины, линиями – ребра графа. В кружках обозначены номера вершин, над ребрами обозначена их вес – (или длина пути).

Рядом с каждой вершиной обозначена метка – длина кратчайшего пути в эту вершину из вершины 1.

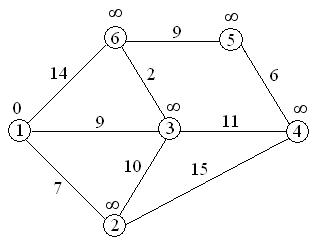
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.

7<¥, поэтому метка ¥ при вершине 2 заменяется меткой 7,

9<¥, поэтому метка ¥ при вершине 3 заменяется меткой 9,

14<¥, поэтому метка ¥ при вершине 6 заменяется меткой 14,

вершина 1 вычеркивается из числа посещенных вершин.

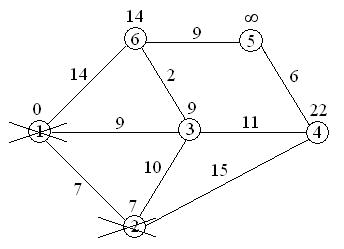
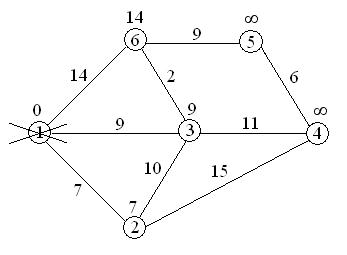
7+10=17>9, поэтому метка 9 при вершине 3 остается;

7+15=22<¥, поэтому метка ¥ при вершине 4 заменяется меткой 22;

вершина 2 вычеркивается из числа посещенных вершин.

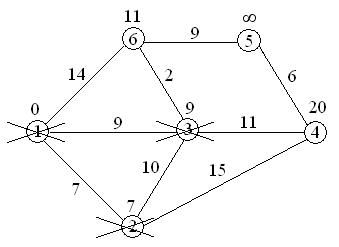
9+11=20<22, поэтому метка 22 при вершине 4 заменяется меткой 20;

9+2=11<14, поэтому метка 14 при вершине 6 заменяется меткой 11;

вершина 3 вычеркивается из числа посещенных вершин.

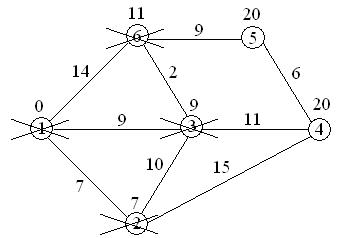
11+9=20<¥, поэтому метка ¥ при вершине 5 заменяется меткой 20;

вершина 6 вычеркивается из числа посещенных вершин.

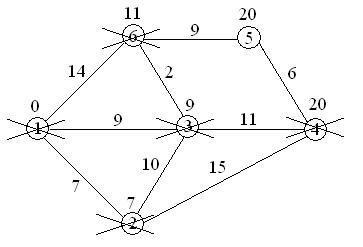
20+6=26>20, поэтому метка 20 при вершине 5 остается;

вершина 4 вычеркивается из числа посещенных вершин.

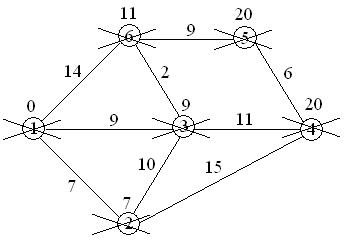
У вершины 5 не посещенных смежных вершин нет, поэтому вершина 5 также вычеркивается из числа не посещенных вершин.

Алгоритм заканчивает работу, так как нельзя больше обработать ни одной вершины. Кратчайшие пути – это последние метки при вершинах.

Дата добавления: 2014-01-03