Лекция № 16

Тема: раскраска графов и карт

Основные вопросы, рассматриваемые на лекции:

1. Раскраска графа. Хроматическое число графа. Теорема Кенига.

2. Раскраска карты. Проблема 4-х красок.

3. О решении проблемы 4-х красок.

Краткое содержание лекционного материала

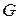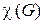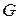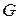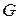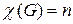1. Раскраска графа. Раскраска карты. - раскраска графа – это приписывание цветов его вершинам, такое, что две любые смежные вершины окрасятся в разные цвета. Граф называется - раскрашиваемым, если его можно окрасить не более чем в цветов. Хроматическим числом графа называется наименьшее число цветов, для которого граф имеет -раскраску. Граф называется - хроматическим, если . Граф 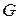являеется - раскрашиваемым, если .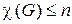

Если граф 1-раскрашиваем, то он вполне несвязен, т.е. не содержит ребер. Значит, 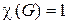тогда и только тогда, когда граф 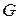вполне не связан.

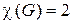тогда и только тогда, когда граф 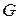не содержит нечетных простых циклов (терема Кенига). Треугольник и 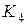являются примерами 3- и 4- хроматического графа. 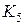не является примером 5- хроматического графа, так как мы рассматриваем только плоские графы. Можно доказать следующую теорему: каждый плоский граф 5-раскрашиваем.

Гипотеза: каждый ли граф 4-раскрашиваем?

2. Раскраска карт. Раскраской плоской карты называется такое приписывание цветов его областям, что никакие две смежные области не получают одинакового цвета. Карта называется - раскрашиваемым, если существует его раскраска, использующая не более чем в цветов. Можно доказать, что каждая плоская карта 5-раскрашиваема.

В 1852 году Френсис Гутри (Guthrie), составляя карту графств Англии, обратил внимание, что для такой цели вполне хватает четырех красок. Его брат, Фредерик, сообщил об этом наблюдении известному математику О. Де Моргану (DeMorgan), а тот - математической общественности. Точная формулировка гипотезы опубликована А. Кэли (Cayley, 1878).

Проблема 4-х красок: достаточно ли 4-х красок для раскраски любой плоской карты.

Заметим, что нетрудно доказать: гипотеза «каждый граф 4-раскрашиваем» равносильна гипотезе 4 красок «каждая плоская карта 4-раскрашиваема».

3. О решении проблемы 4-х красок. В 1976 г К. Аппель и В. Хакен доказали, что четырьмя красками можно раскрасить любую карту. Их доказательство очень объемное, опирается на алгоритмы, реализуемые на компьютерах, в нем все вычисления человеку невозможно проверить.

Дата добавления: 2014-01-03