
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Композиция функций
|
|
|
|
Так как всякая функция – это бинарное отношение, можно строить композицию функций, как композицию бинарных отношений.
Если f: X ® Z (z = f (x)) и g: Z ® Y (y = g (z)), их композиция f g определяется обычным образом,
g определяется обычным образом,
f g = {(x, y) | x Î X, y Î Y, (
g = {(x, y) | x Î X, y Î Y, (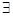 z Î Z): (x, z)Î f и (z, y)Î g }.
z Î Z): (x, z)Î f и (z, y)Î g }.
Учитывая, что f и g – функции, можно записать f g = {(x, y) | x Î X, y Î Y, (
g = {(x, y) | x Î X, y Î Y, (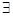 z Î Z): (x, z)Î f и (z, y)Î g } = {(x, y) | (
z Î Z): (x, z)Î f и (z, y)Î g } = {(x, y) | (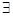 z): z = f (x) и y = g (z)} = {(x, y) | y = g (f (x))}.
z): z = f (x) и y = g (z)} = {(x, y) | y = g (f (x))}.
Теперь видно, что композиция функций – не просто бинарное отношение, а тоже функция, отображающая множество Х в множество Y.
Пример.
Пусть f (x) = 2 x + 1, g (x) = 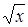 .
.
Найти f  g, g
g, g f и f
f и f  f. Указать области определения и области значений этих функций.
f. Указать области определения и области значений этих функций.
Решение.
(f  g)(x) = g (f (x)) =
g)(x) = g (f (x)) =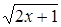 ,
,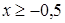 , (f
, (f  g)(x) ³ 0;
g)(x) ³ 0;
(g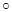 f)(x) = f (g (x)) = 2
f)(x) = f (g (x)) = 2 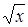 + 1 ,
+ 1 ,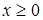 , (g
, (g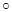 f)(x) ³ 1.
f)(x) ³ 1.
Композиция - некоммутативная операция,
f g (x) ≠ g
g (x) ≠ g f (x).
f (x).
Покажем, что для композиции справедлив закон ассоциативности.
Пусть f, g, h - три функции с согласованными областями определений и значений, так что их композицию можно найти. Тогда
(f  g)
g)  h (x) = h (f
h (x) = h (f  g (x)) = h (g (f (x)))
g (x)) = h (g (f (x)))
f (g
(g h)(x) = (g
h)(x) = (g h)(f (x)) = h (g (f (x)))
h)(f (x)) = h (g (f (x)))
Закон ассоциативности справедлив для любого числа функций. Та единственная функция, которая есть результат композиции функций f 1, f 2, f 3, …, fn (в указанном порядке), так и обозначается:
f 1  f 2
f 2  f 3
f 3  …
…  fn.
fn.
Пример.
Найти все композиции функций f 1 = x 2, f 2 = sin(x), f 3 = x 3 – 1
f 1  f 2
f 2  f3 = (sin(x 2))3 – 1, f 1
f3 = (sin(x 2))3 – 1, f 1  f 3
f 3  f 2 = sin(x 6 – 1), f 2
f 2 = sin(x 6 – 1), f 2  f 1
f 1  f 3 = sin6(x) – 1,
f 3 = sin6(x) – 1,
f 2  f 3
f 3  f 1 = (sin3(x) - 1)2, f 3
f 1 = (sin3(x) - 1)2, f 3  f 1
f 1  f 2 = sin(x 3 – 1)2, f 3
f 2 = sin(x 3 – 1)2, f 3  f 2
f 2  f 1 = sin2(x 3 – 1).
f 1 = sin2(x 3 – 1).
Положим теперь, что f и g - биекции. Если z = f (x), то
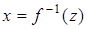 – биекция. Если y = g (z), то z =
– биекция. Если y = g (z), то z = 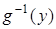 – биекция. Выясним, какими свойствами обладает композиция биекций.
– биекция. Выясним, какими свойствами обладает композиция биекций.
Утверждение.
Композиция взаимно однозначных функций – взаимно однозначная функция, при этом 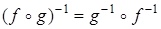 .
.
Доказательство.
1. 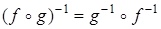 в силу доказанного в лекции 1.4 свойства композиции всяких бинарных от ношений.
в силу доказанного в лекции 1.4 свойства композиции всяких бинарных от ношений.
2. Допустим, что 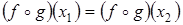 . Тогда g (f (x 1)) = g (f (x 2)) = y. В силу взаимной однозначности функции g f (x 1) = f (x 2). В силу взаимной однозначности функции f x 1 = x 2.
. Тогда g (f (x 1)) = g (f (x 2)) = y. В силу взаимной однозначности функции g f (x 1) = f (x 2). В силу взаимной однозначности функции f x 1 = x 2.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 6770; Нарушение авторских прав?; Мы поможем в написании вашей работы!