Лекция 8. Краткое содержание: Сферическое движение тела

Краткое содержание: Сферическое движение тела. Уравнения движения-углы Эйлера. Теорема Эйлера-Даламбера. Мгновенная ось вращения, угловые скорость и ускорение тела. Скорость и ускорение точки тела.Свободное движение тела. Уравнения движения тела. Скорость и ускорение точки тела.

Движение твердого тела, при котором одна его точка остается неподвижной, называется сферическим движением.

Такое движение совершают, например, волчок, у которого неподвижна точка его опоры, и любое другое тело, закрепленное в какой-либо точке шаровым шарниром.

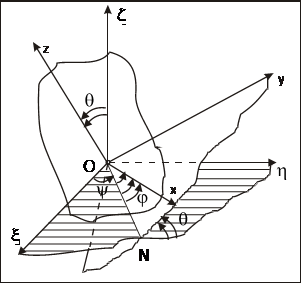Введем две декартовы системы координат: неподвижную 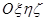и подвижную Охуz с началом в неподвижной точке О.Подвижная система координат Охуz неизменно связана с телом. Плоскость Оху пересекает плоскость 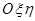по линии ОN, называемой линией узлов.

Положение подвижной системы координат относительно неподвижной определяет положение тело в соответствующий момент времени.

Это положение определяется тремя углами: 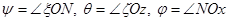, которые называются углами Эйлера.

Угол y, называемый углом прецессии, определяет положение линии узлов ОN относительно неподвижной координатной оси 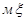. Его изменение характеризует вращение тела с угловой скоростью 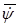относительно неподвижной координатной оси 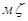, называемой осью прецессии. Угол q, называемый углом нутации, определяет положение подвижной плоскости Оху относительно неподвижной плоскости 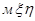(положение подвижной оси Оz относительно неподвижной оси Оz). Его изменение характеризует вращение с угловой скоростью 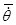относительно линии узлов ОN. Угол j, называемый углом собственного вращения, определяет положение подвижной координатной оси Ох относительно линии узлов ОN. Его изменение характеризует вращение тела с угловой скоростью 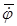относительно подвижной координатной оси Оz, называемой осью собственного вращения.

Таким образом, с помощью трех независимых друг от друга углов Эйлера, которые являются функциями времени и обобщенными координатами, определяется положение подвижной системы координат относительно неподвижной, а, следовательно, и положение тела в любой момент времени.

y=y(t), q=q(t), j=j(t). (*)

Эти функции, являющиеся уравнениями движения тела, должны быть однозначными, непрерывными и дважды дифференцируемыми функциями.

Теорема Эйлера-Даламбера: Перемещение тела, имеющего одну неподвижную точку, из одного положения в другое можно осуществить одним поворотом вокруг оси, проходящей через эту точку и называемую осью конечного поворота.

Траектории точек, принадлежащих телу, имеющему одну неподвижную точку, лежат на концентрических сферах, центр которых совпадает с неподвижной точкой О, а радиус равен расстоянию от точек до неподвижной точки О (отсюда название – сферическое движение).

Положение тела, имеющего неподвижную точку, относительно некоторой системы отсчета можно полностью определить положением сферической фигуры, получающейся в сечении тело одной из вышеназванных сфер.

Положение на этой сфере сферической фигуры полностью определяется заданием на этой сферической фигуре двух точек или дуги большого круга, проходящей через эти точки. Поэтому доказательство теоремы Эйлера-Даламбера повторяет метод доказательства теоремы 2 о перемещении плоской фигуры с той лишь разницей, что доказательство ведется не на плоскости с прямолинейным отрезком, а на сфере с дугой большого круга.

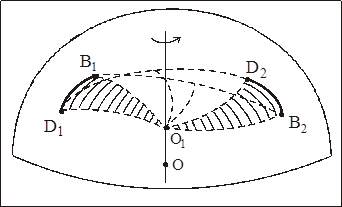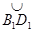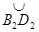Доказательство: Пусть дуги большого круга и определяют положение дуги 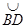на сферическом сечении тело в моменты времени t₁ и t₂ соответственно.

Соединив точки B₁ и D₁ соответственно с точками В₂ и D₂ дугами большого круга, восстановим в серединах дуг 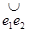и 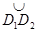сферические перпендикуляры, касательные к которым перпендикулярны соответственно касательным, проведенным в серединах дуг 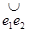и 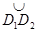. Эти сферические перпендикуляры пересекутся в точке O₁ сферы. Ось ОO₁ – неподвижная ось вращения. Так как 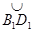=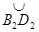, а также равны сферические наклонные равноудаленные от сферических перпендикуляров: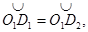 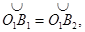то сферический треугольник O₁B₁D₁ равен сферическому треугольнику O₁B₂D₂. Следовательно, сферический угол B₁O₁D₁ равен сферическому углу B₂O₁D_2. После поворота сферического треугольника O₁B₁D₁ вокруг оси ОO₁ на сферический угол D₁O₁D₂ дуга большого круга 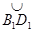совпадет с дугой большого круга 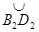, так как сферические углы D₁O₁D₂ и В₁O₁В₂ равны: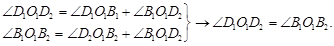

Таким образом, перемещение дуги большого круга 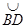(следовательно, и тело) из положения 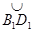в положение 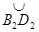осуществлено одним поворотом вокруг оси, проходящей через неподвижную точку О.

Дата добавления: 2014-01-03