Представление результата измерения в виде оценки среднего значения и ее стандартного отклонения

Синтез эффективной оценки среднего значения результата измерения

Анализ апостериорной информации: выдвижение и проверки гипотез о законе распределения вероятности результата измерения

Исключение поправок

Внесение в показание поправок и получение независимых значений результата измерения

Перевод всех значений отсчета в значения показания

После анализа априорной информации и тщательной подготовки к измерению получают n независимых значений отсчета, являющегося случайным числом, проще всего получить путем многократного повторения операции сравнения с помощью одного и того же средства измерений.

Анализ априорной информации; определение поправок

Выполнение измерительных процедур; получение независимых значений отсчета

Вычисление доверительных границ результата измерения с учетом неисключенных систематических погрешностей.

Систематические погрешности должны быть определены и исключены (в виде поправок) из результатов наблюдений на первом этапе обработки данных.

Однако могут быть такие случаи, когда можно только сказать, что систематическая погрешность имеется, но определить ее величину и исключить из результата измерения нельзя. Так бывает, если, например, в расчетную формулу входят постоянные величины (коэффициент и слагаемые), известные с ограниченной точностью. К этому типу погрешностей могут быть отнесены и систематические погрешности средств измерения и изменение параметров объектов измерения.

Таким образом, погрешность результата измерения может включать также значимые неисключенные систематические погрешности. При суммировании неисключенных систематических погрешностей они рассматриваются как случайные величины с равномерным распределением.

Порядок расчетов при этом имеет следующий вид:

1. Определяют абсолютные величины неисключенных систематических погрешностей.

При отсутствии более точных данных они могут быть оценены следующим образом:

1) Погрешности постоянных величин, входящих в формулу, равны половине единицы последнего разряда;

2) Приборная погрешность в некоторых случаях может быть принята равной цене деления (или 1/2 цены деления) шкалы прибора;

3) В других случаях она указывается в паспортных данных измерительных средств.

2. Проводят сложение всех неисключенных систематических погрешностей и определение суммарной неисключенной систематической погрешности.

Если неисключенные систематические погрешности определяются погрешностями постоянных величин, входящих в формулу в виде сомножителей, то суммарная неисключенная погрешность определяется по формуле:

q = 1,1 Х_n Ö (q₁/ W₁)² + (q₂/ W₂)² +..... + (q_m/ W_m)²

Если источниками ошибок являются слагаемые, то суммирование проводят по формуле:

q = 1,1 Ö q₁² + q₂² +....+ q_m² (для Р = 0,95 К = 1,1),

где q - суммарная неисключенная погрешность; q₁, q₂,... q_n - неисключенные систематические погрешности W₁, W₂, W_m.

3. Суммарную неисключенную систематическую погрешность сревнивают со средним квадратическим отклонением результата измерений S(Х).

Если q / S(Х) £ 0,8, то неисключенные систематические погрешности можно не учитывать, т.е. в этом случае суммарная погрешность результата измерения определяется случайной погрешностью: d_å = e.

Если q/ S(Х) > 8, то суммарная погрешность результата измерения целиком определяется неисключенными систематическими погрешностями, и случайные погрешности можно не учитывать (например, в случае технических измерений).

Если q/ S(Х) лежит в диапазоне 0,8 ¸ 8, то при определении суммарной погрешности результата измерения необходимо учитывать как неисключенные систематические, так и случайные погрешности. В этом случае проводят расчет по п.4.

4. Вычисляют суммарное среднее квадратическое отклонение результата измерения:

S_å = Ö q₁²/3 + q₂²/3 +.....+ q_m²/3 + S²(Х),

где q₁, q₂,.... q_m - систематическая погрешность резных видов; S(Х) - среднее квадратичное отклонение результата измерения.

5. Вычисляют коэффициент К: К=(e + q)/(S(Х) + Ö q₁²/3 + q₂²/3 +.....+ q_m²/3)

где e - случайная погрешность результата измерения.

6. Вычисляют суммарную погрешность результата измерения d:

d = К S

7. Результат измерения записывают в виде:а = Х ± d (Р = 0.95)

Запись означает, что истинное значение измеряемой величины с вероятностью не менее Р лежит в пределах от Х + d до Х - d.

Из формул и существа понятия неисключаемой систематической погрешности следует невозможность повышения точности измерений, сужения доверительных границ суммарной погрешности свыше определенного уровня (например, меньше цены деления шкалы средства измерения) путем увеличения числа параллельных определений. В этом случае будет уменьшаться только случайная составляющая суммарной погрешности (теоретически до нуля).

Определение количества параллельных наблюдений для получения результата измерения с погрешностью не выше заданной.

Могут быть два варианта решения поставленного вопроса в зависимости от того, учитываются или нет неисключенные систематические погрешности.

1 случай. Когда неисключенная систематическая погрешность мала, т.е. суммарная погрешность определяется случайными погрешностями, число параллельных определений n, которые необходимо выполнить для получения результата с погрешностью, не превышающей ± e, определяется следующим образом:

1. Задаются необходимой степенью надежности оценки погрешности. Для технических расчетов обычно Р = 0,95.

2. Оценивают среднее квадратическое отклонение ожидаемого результата наблюдения (S).

Для определений по методике с известным относительным средним квадратическим отклонением (S_r): S = S_r×Х, где Х - примерное значение определяемого результата.

3. По таблице функции Лапласа находят u_P, соответствующее принятому Р. Для Р = 0,95 u_P = 2,0

4. Находят необходимое число параллельных определений, при котором с принятой вероятностью Р случайная погрешность не превысит ± e:

n = (u_P S / e)²

Для Р = 0,95 формула 24 принимает вид:

n = (2S / e)²

При дробных значениях величину n всегда округляют в большую сторону.

Если S рассчитано при небольшом объеме исходных данных (N < 20), то формула 25 принимает вид:

n = (t_P,f S_N / e)²,

где t_P,f - коэффициент Стьюдента, определяемый для принятой погрешности по таблице, N - число определений по которому рассчитано значение S_N.

П случай. Когда известна неисключенная систематическая погрешность, при определении количества параллельных измерений следует учитывать, что уменьшение случайной погрешности до значения, меньшего, чем 1/5 неисключенной систематической погрешности, уже не будет влиять на суммарную погрешность результата. Поэтому дальнейшее увеличение количества параллельных определений с этой точки зрения нецелесообразно.

Порядок определения количества параллельных измерений в этом случае:

1. Определяют суммарную неисключенную погрешность. При наличии нескольких источников погрешностей проводят суммирование погрешностей по формулам 20-22.

2. Определяют минимальную оправданную случайную погрешность:

e_n = 0,2 × q, т.е. 1/5 от неисключенной систематической погрешности.

По формулам 24-26 определяют количество параллельных измерений, которое обеспечивает получение принятого значения e_n.

Влияние объема выборки на количество и стабильность показателей, получаемых при статистическом анализе.

Это влияние можно охарактеризовать с помощью таблицы 1.

Таблица 1.

Влияние объема выборки на количество и стабильность показателей

П о к а з а т е л ь	Тенденции изменения при увеличении объема выборки
Среднее арифметическое (результат измерения) - Х	Хаотически колеблется, но постепенно стабилизируется и приближается к своему пределу - генеральному среднему - m
Среднее квадратическое отклонение результата единичного измерения - Sn	Сначала хаотически колеблется, но постепенно стабилизируется и приближается к своему пределу - генеральному среднему квадратическому отклонению - s
Среднее квадратическое отклонение результата измерения - S(Х) и случайная погрешность результата измерения - e	Колеблется, но медленно уменьшается (в пределе до нуля для бесконечно большой выборки - генеральной совокупности)
Неисключенная систематическая погрешность - q	Не изменяется
Суммарная погрешность результата измерения - d	Сначала может колебаться, затем уменьшается до уровня неисключенной систематической погрешности и далее не изменяется

Этапы обработки данных:

1) первичная обработка данных

2) описание данных

3) исследование зависимостей (связь между измеряемыми зависимыми величинами (откликами) и независимыми измеряемыми величинами (факторами). При этом если погрешность факторов незначима, то исследование зависимости называется регрессионным анализом и дисперсионным анализом, когда погрешности откликов и факторов значимы. Математическое выражение зависимости называется целевым уравнением, включающим и базисные уравнения (например, уравнение материального баланса). Константы, входящие в целевое уравнение называются параметрами.

При проведении измерений необходимо стремиться к обеспечению оптимальной точности результата измерений. При этом следует помнить, что низкая точность измерений приводит к получению ошибочной информации о состоянии измеряемого объекта. Необоснованно высокая точность измерения может быть экономически неоправданной. Поэтому при решении вопроса о выборе средств и методов измерений следует помнить следующие основные положения:

1. Средства измерений не должны оказывать влияние на физическое состояние измеряемого объекта.

2. При выборе измерительной базы необходимо исходить из цели измерений и их назначения. Так, при исследовании эксплуатационных параметров объекта в качестве базы для измерений следует принимать эксплуатационную базу. Тогда как при исследовании точности технологического процесса базой измерений должна явиться технологическая база, которая используется при изготовлении измеряемого объекта.

3. Во всех случаях точность относительного (дифференциального) измерения выше точности абсолютного измерения. Поэтому, когда абсолютные измерения не позволяют получить результаты с необходимой точностью, следует перейти к относительным измерениям как одному из способов получения результата измерений с более высокой точностью.

4.Повышение точности результата измерений может быть достигнуто исключением грубых и систематических погрешностей из результатов измерений и уменьшением влияния случайных погрешностей. При этом во всех случаях грубые погрешности (промахи) следует исключать из результатов измерений. Систематические погрешности следует исключать тогда, когда это обеспечивает заметное повышение точности. Необходимо иметь в виду, что, если принять за результат измерений среднее арифметическое из ряда n-измерений, точность повышается в n^0.5 раз.

5. Зависимость между s_х и s единичных измерений определяется равенством

s_о =s_х/Ön

В связи с тем, что точность измерений частоты выше точности измерения любой другой физической величины, следует стремиться выбирать такой метод измерений, который позволяет измеряемую величину преобразовать в частоту (s_о² =s_х²/n)

6. Неоднородность измеряемого объекта не должна оказывать влияние на результат его измерений. Поэтому путём обработки результатов измерений следует исключить влияние неоднородности.

7. Необходимо помнить, что порог чувствительности средств измерений (для меры это будет точность её аттестации) ограничивает возможная точность результата измерений. Точность результата измерений никогда не может быть выше порога чувствительности средств измерений.

ПРИЛОЖЕНИЕ 2

Статистические критерии. Для данных, измеренных в шкале отношений, для проверки гипотезы о совпадении характеристик двух групп целесообразно использование либо критерия Крамера-Уэлча, либо критерия Вилкоксона-Манна-Уитни. Критерий Крамера-Уэлча предназначен для проверки гипотезы о равенстве средних (строго говоря – математических ожиданий) двух выборок, критерий Вилкоксона-Манна-Уитни (плохо применим в условиях, когда число отличающихся друг от друга значений в выборках мало) является более "тонким", но и более трудоемким – он позволяет проверять гипотезу о том, что две выборки "одинаковы", в том числе, что совпадают их средние, дисперсии и все другие показатели (две выборки могут иметь одинаковые средние (то есть, критерий Крамера-Уэлча установит совпадение средних), но различаться, например, разбросом. Те различия, которые не выявит критерий Крамера-Уэлча, могут быть выявлены критерием Вилкоксона-Манна-Уитни).

Критерий Крамера-Уэлча. Эмпирическое значение данного критерия рассчитывается на основании информации об объемах N и М выборок x и y, выборочных средних x и y и выборочных дисперсиях D_x и D_y сравниваемых выборок (эти значения могут быть вычислены вручную по формуле: Тэмп =

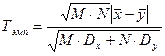
Алгоритм определения достоверности совпадений и различий характеристик сравниваемых выборок для экспериментальных данных, измеренных в шкале отношений, с помощью критерия Крамера-Уэлча заключается в следующем:

1. Вычислить для сравниваемых выборок Tэмп – эмпирическое значение критерия Крамера-Уэлча по формуле (3).

2. Сравнить это значение с критическим значением T_0.05 = 1,96: если Tэмп ≤ 1,96, то сделать вывод: "характеристики сравниваемых выборок совпадают на уровне значимости 0,05"; если Tэмп > 1,96, то сделать вывод "достоверность различий характеристик сравниваемых выборок составляет 95%".

Критерий Крамера-Уэлча является более эффективным "заменителем" такого известного в физике и технике критерия как t-критерий (критерий Стьюдента).

Дата добавления: 2014-01-03