Внутренняя энергия и энтальпия рабочего тела как функция состояния

Внутренняя энергия U является экстенсивным свойством газа, т.е. зависит от его массы (в противоположность свойствам, не зависящим от массы и называемым интенсивными). Поэтому для большей определенности внутреннюю энергию газа обычно относят к единице массы (1кг). Такая удельная внутренняя энергия обозначается буквой u. Таким образом, если масса рассматриваемого газа равна М кг, то

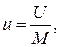Дж/кг. (1.5)

Из самого определения внутренней энергии вытекает, что каждому состоянию газа соответствует одно и только одно значение внутренней энергии. Это означает, что внутренняя энергия представляет собой однозначную функцию состояния или, иначе, однозначную функцию любых двух независимых параметров, определяющих это состояние.

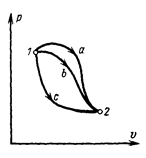
Поэтому изменение внутренней энергии в каком – либо процессе не зависти от характера процесса, а однозначно определяется заданными начальным и конечным состояниями газа. Так, в процессах а,b и с (рис 1.1.), в которых начальные и конечные состояния газа одинаковы, одинаковыми будут и изменения внутренней энергии :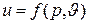

.

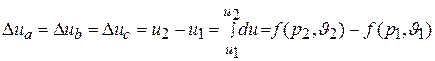Математически это означает, что дифференциал du является полным дифференциалом функции 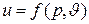и может быть представлен равенством

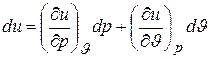. (1.6)

Очевидно, что если процесс замкнут, т.е. если после завершения его газ возвращается в исходное состояние (такие процессы в термодинамике называются круговыми процессами или циклами), то изменение внутренней энергии в нем будет равно нулю:

.

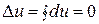Как нетрудно видеть, аналогичными свойствами обладают все рассмотренные выше параметры: p, 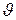и Т. Следовательно, и внутренняя энергия может служить параметром состояния газа. Как и все другие параметры состояния, измеряемые в тепловых единицах (Дж), она относится к калорическим параметрам, а уравнение состояния, в состав которого входит внутренняя энергия (или какой – либо другой калорический параметр), например уравнение

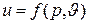
называется калорическим уравнением состояния.

Наряду с внутренней энергией в дальнейшем изложении основ технической термодинамики важную роль играет величина

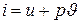, кДж/кг, (1.7)

называемая энтальпией газа. Будучи составленной из функций состояния, энтальпия сама является функцией состояния и играет роль одного из калорических параметров состояния. Очевидно, что все свойства функции состояния имеет и энтальпия. Например, если задана зависимость 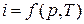,то

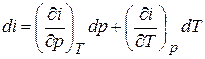, (1.8)

т.е. дифференциал энтальпии является полным дифференциалом.

Равным образом, для цикла

,

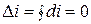а для незамкнутого процесса 1–2

,

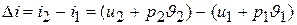независимо от пути, по которому протекает процесс.

Энтальпия представляет собой в общем случае чисто математическую величину и приобретает конкретный физический смысл лишь применительно к процессам, протекающим в газовом потоке, которые будут рассматриваться ниже.

Дата добавления: 2014-01-03