Основные определения. Теплоемкостью тела в каком – либо процессе изменения его состояния называется количество тепла, потребное для повышения его температуры на один градус

Теплоемкостью тела в каком – либо процессе изменения его состояния называется количество тепла, потребное для повышения его температуры на один градус. Теплоемкость, отнесенная к единице количества вещества, является его удельной теплоемкостью, однако обычно ее также называют просто теплоемкостью. Применительно к газам в технической термодинамике различают массовую теплоемкость с, кДж/(кг·град), объемную теплоемкость с^/, кДж/(м³×град) и мольную теплоемкость

, кДж/(кмоль×град). Между собой эти теплоемкости связаны очевидными соотношениями:

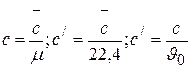, (3.1)

где 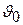– удельный объем при нормальных условиях.

Как было показано выше, тепло является функцией процесса, поэтому понятие теплоемкости имеет смысл лишь в том случае, когда задан характер процесса, в котором газу сообщается тепло. Соблюдение же этого условия устанавливает однозначную связь между теплом процесса и температурой газа, которую можно выразить уравнением

,

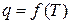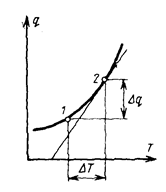
или представить графически в виде некоторой кривой (рис. 3.1).

Очевидно, что на различных участках такой кривой одному и тому же изменению температуры соответствуют различные количества подведенного тепла, поэтому и значения теплоемкости на этих участках будут различными. В связи с этим приходится ввести понятие о теплоемкости, средней в заданном интервале температур от Т₁ до Т₂ (т.е. на участке 1–2 кривой, изображенной на рис. 3.1).

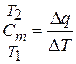. (3.2)

Беспредельно уменьшая рассматриваемый температурный интервал, получаем значение истинной теплоемкости при заданной температуре:

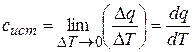. (3.3)

Таким образом, истинная теплоемкость при данной температуре представляет собой предел, к которому стремится теплоемкость, средняя для прилегающего температурного интервала, когда этот интервал стремится к нулю. Это означает, что истинная теплоемкость математически выражается как первая производная тепла по температуре (при условии, что задан характер процесса и этим определена функциональная зависимость между теплом и температурой).

Характер процесса может быть задан постоянством какого – либо из параметров газа в нем, что в общем виде выражается формулой x = const. В этом случае теплоемкость газа представляет собой частную производную

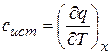(3.4)

и никаких дополнительных условий для ее определения не требуется, поскольку уже само условие x = const устанавливает необходимую функциональную зависимость тепла от температуры.

3.2 Теплоемкости с_J и с_р

В технической термодинамике особо важную роль играют теплоемкости при постоянном объеме

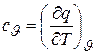(3.5)

и теплоемкости при постоянном давлении

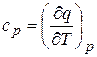(3.6)

Связь между ними легко устанавливается из первого закона термодинамики, согласно которому

.

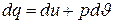Если тепло подводится при постоянном объеме, то 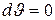, а следовательно,

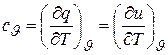. (3.7)

Если тепло подводится при постоянном давлении, то

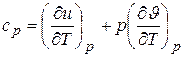. (3.8)

Для идеального газа эти выражения упрощаются. Поскольку его молекулы не связаны силами взаимодействия, его внутренняя энергия u не зависит ни от объема, ни от давления, следовательно,

.

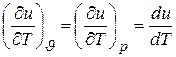Кроме того, из уравнения состояния идеального газа 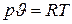имеем

.

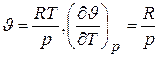Отсюда получаем

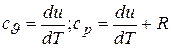
и окончательно 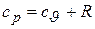. (3.9)

Полученная формула называется уравнением Майера.

Умножая обе части уравнения Майера на молекулярную массу m, получаем аналогичную зависимость для мольных теплоемкостей идеального газа

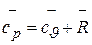. (3.10)

3.3 Молекулярно – кинетическая теория теплоемкости

Численные значения теплоемкости идеальных газов могут быть получены из основного уравнения кинетической теории газов (2.1) путем следующих несложных преобразований.

Умножая обе части этого уравнения на объем одного киломоля 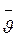, получаем

,

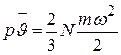где 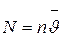– число молекул в одном киломоле газа, называемое числом Авогадро и равен 6,032×10²⁶.

Если молекулы газа представить себе в виде материальных точек, могущих совершать только поступательное движение, то внутренняя энергия одного киломоля будет равна

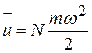
и следовательно, .

Один из основных законов кинетической теории газов гласит, что внутренняя энергия газа распределяется равномерно между степенями свободы движения молекул. Материальная точка имеет три степени свободы, следовательно, на каждую из них в одном киломоле газа приходится внутренняя энер

гия, равная .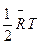

Однако, материальной точкой можно считать молекулу только одноатомного газа; если же молекула состоит из двух или более атомов, то число степеней свободы ее составляют 3+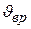, где J_вр – число степей свободы вращательного движения молекул, причем для двух атомных газов J_вр = 2, а для трех атомных газов J_вр = 3.

Таким образом, в общем виде внутренняя энергия одного киломоля газа выражается формулой

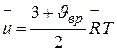. (3.11)

Если газ нагревается при постоянном объеме, то он работы не совершает, а потому, согласно первому закону термодинамики, все затраченное тепло расходуется на изменение внутренней энергии и, следовательно

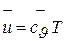. (3.12)

Отсюда получаем

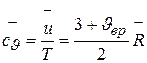. (3.13)

Ранее было показано, что между мольными теплоемкостями идеального газа существует связь, выражающаяся формулой (3.10), следовательно,

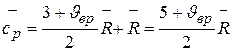. (3.14)

Формулы (3.13) и (3.14) показывают, что согласно молекулярно – кинетической теории газов теплоемкости их в процессах с постоянным объемом и с постоянным давлением являются величинами постоянными.

Дата добавления: 2014-01-03