Зависимость теплоемкости от температуры

Полученные выше на основании кинетической теории газов численные значения теплоемкостей пригодны только для грубых расчетов, да и то лишь в области низких температур, т.е. когда внутримолекулярные колебания атомов несущественны. В точных расчетах, особенно при высоких температурах, необходимо учитывать энергию колебательного движения атомов, которая является функцией температуры.

Колебательная составляющая теплоемкости может быть получена с помощью квантовой теории, которая приводит к следующему выражению, называемому формулой Эйнштейна

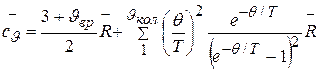, (3.15)

где 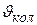– число степеней свободы внутримолекулярных колебаний;

q – характеристическая температура внутримолекулярного колебательного движения, прямо пропорциональная частоте внутримолекулярных колебаний

е – основание натуральных логарифмов.

Первый член формулы Эйнштейна дает постоянное, не зависящее от температуры приближенное значение теплоемкости, которое учитывает только энергию поступательного и вращательного движения молекул. Второй член, учитывающий энергию внутримолекулярных колебаний, вычисляется на основании экспериментальных спектроскопических данных, характеризующих частоты внутримолекулярных колебаний.

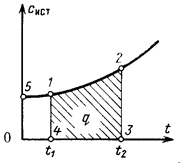При этом оказывается, что зависимость теплоемкости от температуры у двух–, а, особенно у трех– и многоатомных газов весьма существенна и может быть изображена для каждого конкретного процесса в виде возрастающей кривой, обращенной выпуклостью вниз (рис. 3.2).

Естественно, что для каждого конкретного процесса (например, для процесса при 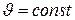или процесса при p = const) получается своя кривая. Однако в каждом конкретном случае характер процесса устанавливает необходимую функциональную связь между теплом и температурой, а потому истинную теплоемкость можно считать производной тепла по температуре. Поскольку при этом 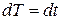, из формулы (3.3) получаем

,

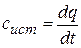ил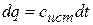и и 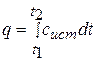. (3.16)

Полученная формула показывает, что тепло q, затраченное на осуществление заданного процесса нагрева от температуры t₁ до t₂ графически изображается площадью 1– 2– 3– 4– 1, лежащей под кривой зависимости .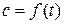

Для аналитического вычисления этого тепла нужно знать зависимость 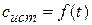. Обычно она выражается степенной формулой

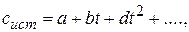(3.17)

численные коэффициенты которой подбираются с таким расчетом, чтобы полученные по этой формуле значения теплоемкостей были как можно ближе к тем, которые дает экспериментальный график.

Однако вычисление количества тепла по формуле

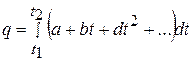
связанное с интегрированием довольно сложного выражения, весьма трудоемко и практически не осуществляется. Необходимый результат может быть получен и другим способом.

Из графика зависимости 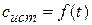видно, что тепло, затраченное на нагревание газа от t₁ до t₂

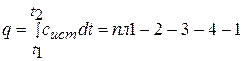
что можно представить в таком виде

,

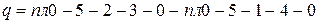или учитывая, что на оси ординат t=0

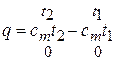. (3.18)

Применение этой формулы весьма удобно при наличии данных по средним теплоемкостям 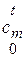. Современная теплотехника располагает такими данными, полученными на основе точных экспериментов. Они сведены в таблицы теплоемкостей, которые и используются для теплотехнических расчетов.

В таблицах значения теплоемкостей 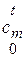даны с интервалом 100⁰. Теплоемкости для температур, не кратных 100⁰, находятся путем интерполирования.

В некоторых случаях требуется, пользуясь таблицей теплоемкостей 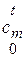, найти значения теплоемкости 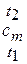. Нетрудно видеть, что для этого можно воспользоваться формулой

.

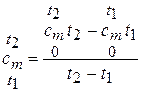Дата добавления: 2014-01-03