Адиабатный процесс

Адиабатным называется равновесный процесс, протекающий без теплообмена между рабочим телом и окружающей средой. Уравнение адиабаты (линии, изображающие адиабатный процесс графически) в 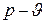диаграмме может быть получено из аналитических выражений первого закона термодинамики, которые в данном случае принимают вид

и .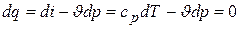

Из этих уравнений имеем

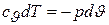и .

Разделив второе равенство на первое, получаем

.

Это отношение представляет собой важную характеристику адиабатного процесса, обозначаемую буквой k. Таким образом,

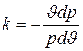
или .

Интегрируя это дифференциальное уравнение, получаем

,

или 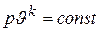(4.14)

Полученное соотношение называется уравнением Пуассона и выражает аналитическую связь между параметрами р и J в адиабатном процессе, а потому представляет собой уравнение адиабаты в диаграмме. Входящая в него величина k называется показателем адиабаты. Графически адиабата изображается линией 1–2, схожей с гиперболой, но расположенной несколько круче (рис. 4.4).

Дифференцируя уравнение изотермы (4.11^/), получаем

,

откуда угловой коэффициент (тангенс угла наклона) касательной к изотерме

.

С другой стороны, дифференцируя уравнение (4.14), получаем

,

откуда угловой коэффициент касательной к адиабате

.

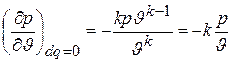Поскольку всегда k > 1,

,

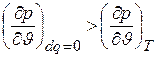т.е. действительно, адиабата в в 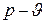диаграмме круче изотермы.

В адиабатном процессе все три термических параметра () переменны, поэтому связь между их значениями для начального конечного состояния газа выражается тремя уравнениями.

а) Связь между параметрами р и J. Из уравнения адиабаты (4.14) имеем

.

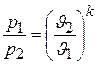б) Связь между параметрами Т и J. Сопоставляя формулы (2.3) и (4.14), получаем

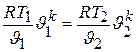или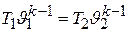

и окончательно

(4.16)

в) Связь между параметрами р и Т. сопоставляя формулы (4.15) и (4.16), получаем

,

откуда находим окончательно

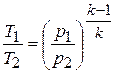. (4.17)

Аналитическое выражение первого закона термодинамики для адиабатного процесса примет вид

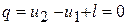
или

. (4.18)

Это означает, что работа изменения объема в адиабатном процессе совершается за счет изменения внутренней энергии. Если газ расширяется и работа положительна, то внутренняя энергия уменьшается; если происходит сжатие и работа газа отрицательна, то внутренняя энергия увеличивается. Поэтому адиабатное расширение сопровождается уменьшением температуры газа, а адиабатное сжатие – ее увеличением.

Поскольку для любого процесса, в том числе и для адиабатного,

,

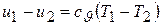работа адиабатного процесса может быть найдена по формуле

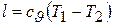. (4.19)

Этой формуле можно придать и другой вид. Поскольку

,

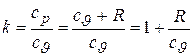имеем

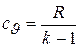
и тогда

. (4.20)

Далее, учитывая формулу (2.3), получаем

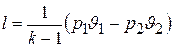. (4.21)

Дата добавления: 2014-01-03