Политропные процессы

Политропными называются процессы, в которых теплоемкость имеет любое, но постоянное на протяжении всего процесса значение. Очевидно, это определение означает, что в любом политропном процессе распределение подводимого тепла между изменением внутренней энергии и работой газа, характеризуемое величиной

,

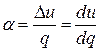остается неизменным, поскольку dq = c×dT и

.

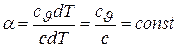Здесь буквой с обозначена постоянная для данного процесса теплоемкость газа.

Уравнение политропы в 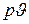–диаграмме может быть выведено из аналитических выражений первого закона термодинамики

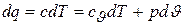
и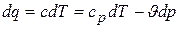

откуда получаем

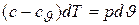и .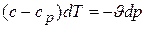

Разделив второе равенство на первое, имеем

.

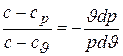Обозначая постоянную для данного процесса величину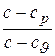через n, получаем

,

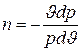а после разделения переменных

.

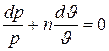Интегрируя полученное дифференциальное уравнение, находим

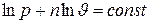
и окончательно

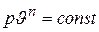. (4.22)

В этом уравнении величина n называется показателем политпропы. Будучи постоянным для каждого конкретного процесса, численное значение этого показателя определяет характер процесса.

Так, при n = 0 уравнение политропы принимает вид

p = const,

т.е. превращается в уравнение изобары. Следовательно, изобара представляет собой политропу с n = 0.

Аналогично этому легко показать, что изотерма – это политропа с показателем n = 1, а адиабата – это политропа с показателем n = k.

Согласно определению политропного процесса изохора также является политропой, поскольку для нее с = с_J = const. Показатель политропы для изохорного процесса можно определить следующим образом.

Из уравнения политропы следует, что

.

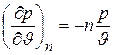Так как для линии J = const должно быть

.

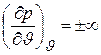То .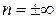

Все соотношения, вытекающие из уравнения политропы 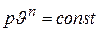, должны быть аналогичными соотношениям, вытекающим из уравнения адиабаты 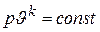, и получаются из них путем замены показателя адиабаты k на показатель политропы n.

Таким образом, связь между параметрами газа в двух состояниях при политропном процессе выражается формулами

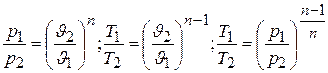, (4.23)

а формулы для работы изменения объема газа в политропном процессе имеют вид

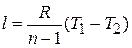(4.24)

и 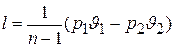. (4.25)

Согласно первому закону термодинамики для политропного процесса

.

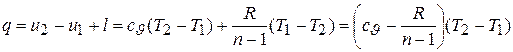Сравнивая полученное выражение с формулой

,

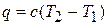находим зависимость

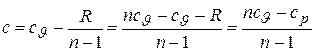
или учитывая, что 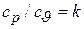, имеем окончательно

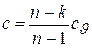. (4.26)

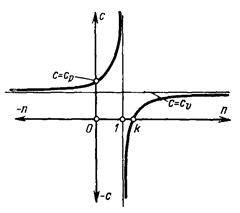Таким образом, в зависимости от показателя политропы теплоемкость газа в политпропных процессах может иметь различные значения, что наглядно иллюстрируется графиком с = f (n), приведенным на рисунке 4.5. В частности, для изохорного процесса, когда 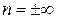, с = с_J; для изобарного процесса, когда n = 0, c = c_p; для изотермического процесса, когда n = 1, 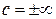; наконец, для адиабатного процесса, когда n = k, c = 0.

Далее график показывает, что на участке 1< n < k, т.е. для политропных процессов, расположенных между изотермой и адиабатой, значение теплоемкости отрицательно. Это объясняется тем, что на указанном участке числитель и знаменатель выражения

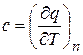
имеют разные знаки.

Действительно, при политропном расширении в этом случае тепло подводится, но температура понижается; при политропном сжатии, наоборот, тепло отводится, но температура повышается.

Логарифмируя уравнение политропы 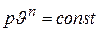, получаем

.

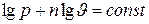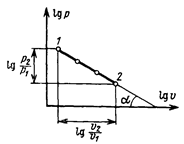Это отношение в логарифмической системе координат изображается прямой линией (например, 1–2 на рис. 4.6). Поэтому, для того чтобы установить, является ли политропным процесс, изображенный в 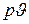–диаграмме какой – либо линией, следует несколько точек этой линии перенести в логарифмическую систему координат. Если все точки расположатся на одной прямой, то график изображает политропный процесс с показателем

.

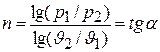Дата добавления: 2014-01-03