Теорема Карно. Приведенное выше выражение для термического к.п.д. цикла Карно было получено исходя из предположения, что рабочим телом двигателя является идеальный газ.

Приведенное выше выражение для термического к.п.д. цикла Карно было получено исходя из предположения, что рабочим телом двигателя является идеальный газ. Чтобы его можно было использовать при анализе циклов с любым другим рабочим телом, следует доказать положение, называемое теоремой Карно и гласящее, что термический к.п.д. обратимого цикла, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего тела, при помощи которого совершается этот цикл.

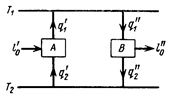Предположим, что между горячим и холодным источниками теплоты (рис. 5.6) с помощью тепловой машины А может быт совершен прямой цикл, в котором рабочее тело получает от горячего источника тепло в количестве q^/₁,отдает холодному источнику тепло в количестве q^/₂ и совершает работу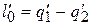 . Термический к.п.д. этого цикла будет равен

.

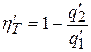Если эта машина будет работать в обратном направлении (как показано на рисунке), то вследствие обратимости цикла рабочее тело будет получать из холодного источника тепло в количестве q^/₂ и отдавать горячему источнику тепло в количестве q^/₁, причем на это будет затрачиваться работа l ^/₀.

Доказательство теоремы Карно получим «методом от противного». Для этого сделаем предположение, что с помощью машины В, в которой используется другое рабочее тело, можно осуществить обратный цикл, термический к.п.д. которого получается большим, чем у цикла машина А, т.е.

.

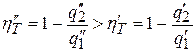Пусть обе машины работают одновременно, причем в машине А совершается обратный цикл, а в машине В – прямой. Подберем количество рабочих тел так, чтобы горячий источник отдавал рабочему телу машины В такое же количество теплоты, какое он получает от рабочего тела машины А, т.е. чтобы .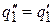

Тогда получаем, что

,

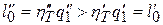поскольку по предположению .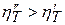

Это означает, что в результате осуществления одновременно двух циклов совершается полезная работа 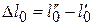. Вместе с тем из неравенства

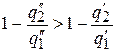
вытекает, что

,

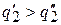т.е., что теплота, отнимаемая от холодного источника рабочим телом машина А, больше, чем теплота, отдаваемая ему рабочим телом машины В на величину

.

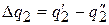Это означает, что единственным результатом одновременного осуществления двух циклов является совершение полезной работы 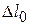за счет теплоты 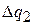, отнимаемой у холодного источника. Полученный результат находится в противоречии со вторым законом термодинамики в формулировке Планка. Вывод, находящийся в противоречии со вторым законом термодинамики, получается и при иных соотношениях между количеством рабочих тел (например, когда они подбираются так, что 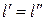или ).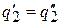

Таким образом, предположение, что можно увеличить термический к.п.д. обратного цикла, взяв другое рабочее тело, приводит к неправильным выводам. Это и является доказательством теоремы Карно.

Дата добавления: 2014-01-03