Энтропия. Следует иметь в виду, что здесь под q2 подразумевается абсолютная величина отводимого тепла

Для прямого цикла Карно (см. рис. 5.4) из формул (5.1) и (5.4) вытекает, что

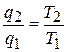или .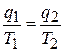

Следует иметь в виду, что здесь под q₂ подразумевается абсолютная величина отводимого тепла. Если учесть, что алгебраически тепло q₂ отрицательно, то последнее равенство надо записать так

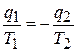или 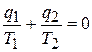. (5.6)

Отношение теплоты к температуре, при которой оно подводится или отводится, называется приведенным теплом. Таким образом, для обратимого цикла Карно алгебраическая сумма теплот равна нулю.

Полученное соотношение можно распространить на любой обратимый цикл (рис. 5.7). Для этого пересечем произвольный обратимый цикл бесконечно 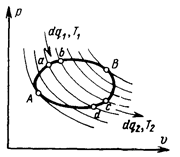большим количеством адиабат и образуем, таким образом, бесконечно большое количество элементарных циклов. В каждом из них (например, в цикле a–b – c –d –a) теплота подводится на верхнем участке в количестве dq₁ при температуре Т₁ и отводится на нижнем участке в количестве dq₂ при температуре Т₂. Изменение температур на этих элементарных участках бесконечно мало, поэтому их можно считать изотермическими, т.е. каждый из полученный элементарных циклов можно считать циклом Карно.

Для каждого из них по уже доказанному можно написать, что

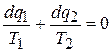. (5.7)

Суммируя все положительные приведенные теплоты, т.е. взяв линейный интеграл величин dq₁/T₁ по верхней линии АВ, а затем, суммируя все отрицательные приведенные теплоты, т.е. взяв линейный интеграл dq₂/T₂ по нижней линии ВА и сложив их, получаем

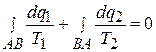
или 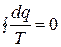, (5.8)

т.е. линейный интеграл элементарных приведенных теплот, взятый по всему контуру рассматриваемого обратимого цикла, равен нулю.

Полученная была выведена Клаузиусом в 1854 г. и носит название интеграл Клаузиуса.

Из математики известно, что если линейный интеграл, взятый по любому замкнутому контуру, равен нулю, то под интегралом находится полный дифференциал, т.е. в данном случае

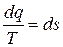, (5.9)

где s – некоторая функция состояния, значение которой однозначно определяется состоянием тела и изменение которой зависит от начального и конечного состояний тела, но не от пути, по которому тело переходит от начального состояния к конечному. Следовательно, если тело переходит из состояния 1 в состояние 2 (рис. 5.8), то по какому бы пути не был осуществлен переход, величина

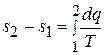(5.10)

будет иметь одно и то же значение. Функция состояния S была названа Клаузиусом энтропией.

Важная роль этой величины в термодинамике определяется тем, что в соответствии с равенством (5.9) изменение ее в любом обратимом процессе является признаком наличия теплообмена между рабочим телом и окружающей средой.

Очевидно, что энтропию можно рассматривать как параметр состояния и, следовательно, изменение ее можно вычислить для любого процесса, если известно изменение двух других параметров состояния, например J и Т, р или р иJ.

Выведем соответствующие зависимости для идеального газа, представив предварительно его уравнение состояния в дифференциальной форме.

Дифференцируя уравнение состояния идеального газа (2.3), получаем

.

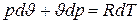Разделив далее левую часть этого уравнения на рJ, а правую на RT (от чего равенство не нарушится), получаем

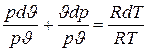
или

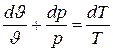. (5.11)

Полученное выражение и является уравнением состояния идеального газа в дифференциальной форме.

Положим теперь, что в качестве независимых переменных заданы J и Т.

На основании первого закона термодинамики

,

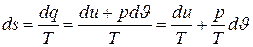поскольку

,

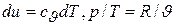получаем

.

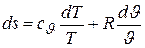Интегрируя данное дифференциальное уравнение, получим искомую зависимость в конечной форме

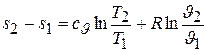. (5.12)

Если в качестве независимых переменных заданы р и Т, то, учитывая, что

,

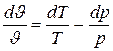получаем

,

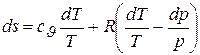или, поскольку с_J+R= с_р, имеем

.

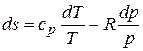Интегрируя, получаем искомую зависимость в конечной форме:

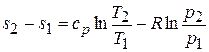. (5.13)

Наконец, если в качестве независимых переменных заданы J и р то, учитывая, что

,

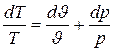получаем

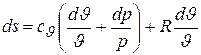
или .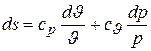

Интегрируя, получаем искомую зависимость в конечной форме

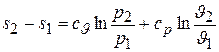. (5.14)

Чтобы определит абсолютное значение энтропии для какого – либо состояния тела, необходимо фиксировать начало ее отсчета. В теплотехнике обычно принимают за такое начало отсчета нормальные условия, т.е. полагают, что при р_о = 760 мм.рт.ст и t_о = 0⁰С энтропия S₀ = 0. Тогда при любых других условиях, заданных параметрами р и Т, значение энтропии можно определить по формуле

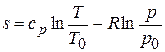. (5.15)

Как видно из всех приведенных выше формул, энтропия имеет ту же размерность, что и массовая теплоемкость, т.е. кДж/(кг× град).

5.7 Ts – диаграмма идеального газа

Из выражения (5.9) получаем формулу dq = Tds, т.е. дифференциальное уравнение для элементарного тела, которое подводится или отводится на бесконечно малом участке процесса, в котором энтропия рабочего тела изменяется на величину ds.

Интегрируя это уравнение, получаем выражение для всего тела процесса, начинающегося от состояния 1 и кончающегося состоянием 2

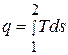. (5.16)

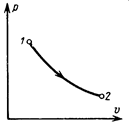
Это выражение показывает, что если изобразить процесс 1-2 в системе координат, в которой по оси абсцисс откладывается энтропия, а по оси ординат – абсолютная температура, то теплота всего процесса будет выражена в ней площадью, соответствующей данному интегралу.

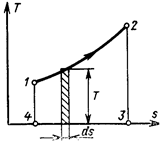Такая система координат находит широкое применение в технической термодинамике и называется Ts – диаграммой (рис. 5.9). Поскольку любое равновесное состояние рабочего тела однозначно определяется значениями двух независимых друг от друга параметров состояния, в данном случае параметров Tи s, очевидно, что каждое из таких состояний изображается в Ts – диаграмме соответствующей точкой, а всякий обратимый процесс – непрерывной линией, например, линия 1-2 изображает в Ts– диаграмме процесс перехода рабочего тела из состояния 1 в состояние 2. элементарное тело этого процесса dq = Tds изображается площадью заштрихованного прямоугольника с высотой,равной Т, и основанием, равным ds, а все тело процесса – площадью 1-2-3-4-1, лежащей между линией процесса 1-2 и осью абсцисс и ограниченной ординатами крайних точек процесса.

Если процесс идет с подводом теплоты, то dq>0, следовательно, и ds>0, (так как Т всегда положительна), т.е. энтропия рабочего тела возрастает и линия процесса в Ts – диаграмме направлена слева направо. Наоборот, если процесс идет с отводом теплоты, то dq<0, следовательно, и ds<0,т.е. энтропия рабочего тела уменьшается и линия про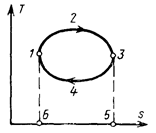цесса направлена справа налево.

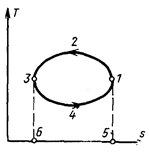
Особенно наглядно в Ts – диаграмме изображаются циклы. Линии циклов в этом случае, как и в рJ – диаграмме, образуют замкнутые контуры, причем линии прямых циклов направлены по часовой стрелке, а обратных – против часовой стрелки. В прямом цикле 1-2-3-4-1 (рис. 5.10) теплота q₁ подводится на верхнем участке цикла 1-2-3, следовательно, подводимое тепло изображается площадью 1-2-3-5-6-1; теплота q₂ отводится на нижнем участке 3-4-1, следовательно, отводимое тепло изображается площадью 3-4-1-6-5-3. значит, полезная теплота q₀ = q₁ –q₂ изображается площадью, ограниченной линией цикла 1-2-3-4-1, а термический к.п.д. представляет собой отношение площади 1-2-3-4-1 к площади 1-2-3-5-6-1. В обратном цикле 1-2-3-4-1 (рис. 5.11) теплота отводится от холодного источника к рабочему телу на нижнем участке 3-4-1, следовательно, теплота q₂ изображается площадью 3-4-1-5-6-3; к горячему приемнику теплота отводится от рабочего тела на верхнем участке 1-2-3, следовательно, теплота q₁ изображается площадью 1-2-3-6-5-1. Значит, работа, затраченная на осуществление цикла, изображается площадью, заключенной внутри контура 1-2-3-4-1.

Рассмотрим изображение в Ts – диаграмме основных процессов идеального газа.

Для изохорного процесса J₁ = J₂, поэтому уравнение (5.12) примет вид

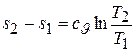. (5.17)

Это уравнение связи между s и T в начальной и конечной точках изохорного процесса легко превратить в уравнение изохоры, если, зафиксировав координаты точки 1, сделать координаты точки 2 текущими, т.е. попросту опустить в них индекс. Тогда получаем формулу

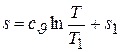, (5.18)

которая и представляет собой уравнение изохоры в Ts – диаграмме.

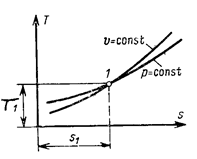Этому уравнению соответствует кривая, проходящая через точку с координатами Т₁ и s₁ (рис. 5.12), которую часто называют логарифмической кривой, хотя по сути дела она является экспонентой.

Аналогичным образом можно получить уравнение изобары. При р = const уравнение (5.13) принимает вид

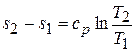, (5.19)

откуда получаем

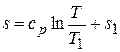. (5.20)

Следовательно, изобара также представляет собой экспоненциальную кривую, проходящую через точку 1. Поскольку с_р>с_J, одному и тому же изменению температуры в изобарном процессе соответствует большее значение энтропии, чем в изохорном. Следовательно, изобара располагается более полого, чем изохора, как и показано на рис. 5.12.

Изотерма, очевидно, представляет собой в Ts – диаграмме горизонтальную прямую.

Адиабата характеризуется равенством dq = 0, следовательно, для нее

,

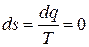т.е. в адиабатном процессе энтропия не изменяется, поэтому адиабата в Ts– диаграмме изображается вертикальной прямой.

Для политропного процесса в общем виде изменение энтропии можно определить на основании равенства

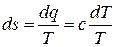, (5.21)

где 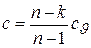– теплоемкость рабочего тела в процессе, показатель политропы которого равен n.

Интегрируя уравнение (5.21), получаем

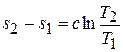, (5.22)

следовательно, уравнение политропы примет вид

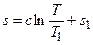. (5.23)

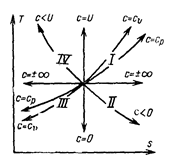Таким образом, все политропы в Ts – диаграмме изображаются экспоненциальными кривыми, принимая для двух частных случаев – изотермы и адиабаты – вид прямых линий (рис. 5.13).

Следует отметить, что в квадрантах I и III dq и dT имеют одинаковые знаки, поэтому теплоемкость

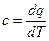
положительна, т.е. с >0; в квадрантах II и IV величины dq и dT имеют разные знаки, поэтому с < 0.

Однако Ts –диаграмма позволяет определить не только знак теплоемкости, но и ее величину. Действительно, если касательная к политропе 1-2 (рис. 5.14) образует с осью абсцисс угол j, то

,

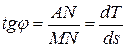откуда

.

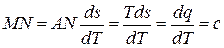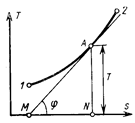Таким образом, массовая теплоемкость рабочего тела в политропном процессе измеряется подкасательной кривой этого процесса в Ts –диаграмме. Если подкасательная расположена влево от точки касания, то теплоемкость положительна, если вправо – то отрицательна.

С помощью Ts – диаграммы можно наглядно представить не только тепло изображенного в ней процесса (измеряемого площадью, расположенной под линией этого процесса), но и изменения в нем внутренней энергии Du и энтальпии Di. Для этого достаточно из начальной точки процесса провести изохору и изобару до пересечения с горизонтальной изотермой, проходящей через конечную точку процесса. Нетрудно видеть, что площади, расположенные под этими линиями, и будут соответствовать искомым значениям Du и Di для рассматриваемого процесса.

Дата добавления: 2014-01-03