Свойства плотности рапределения

1°. Плотность распределения является неотрицательной функцией: р (х) ³ 0 для всех х Î R.

2°. Площадь фигуры, ограниченной графиком плотности распределения и осью абсцисс, равна единице:

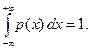(4.3)

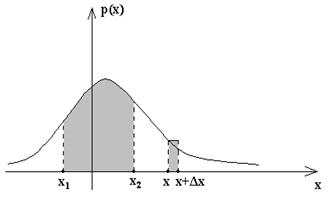
Теорема 4.1. Пусть непрерывная с.в. ξ имеет плотность распределения р (х) и функцию распределения F (х). Обозначим через <х ₁, х ₂ > один из интервалов вида [ х ₁, х ₂], [ х ₁, х ₂), (х ₁, х ₂], (х ₁, х ₂).

Тогда 1) Р {ξ = х ₀} = 0 для любого х ₀Î R; (4.4)

2) Р {ξÎ< х ₁, х ₂>} = F (х ₂) – F (х ₁) =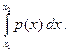 (4.5)

p (x)

Вторая формула в выражении (4.5) имеет простой геометрический смысл: вероятность Р {ξÎ< х ₁, х ₂>} попадания с.в. x в промежуток < х ₁, х ₂> равна площади криволинейной трапеции, ограниченной графиком плотности распределения, осью абсцисс и прямыми х = х ₁, х = х ₂ (рис. 4.1).

x

Рис. 4.1. Геометрическая интерпретация вероятности P {ξ Î < х ₁, х ₂ >}

Пример 4.1. Случайная величина ξ имеет плотность распределения

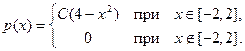
Найти неизвестный коэффициент С, функцию распределения F (х); построить графики функций р (х) и F (х). Вычислить вероятность попадания значения с.в. ξ в промежуток [–1, 1].

Решение. В силу характеристического свойства (4.3) плотности распределения, имеем

1 = 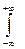р (х) dх = 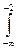0 dх + 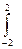С (4– х ²) dх + 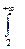0 dх = С 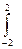(4– х ²) dх = С (4 х – 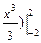= С,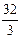

откуда С = 3/32.

Теперь плотность распределения полностью определена:

р (х) =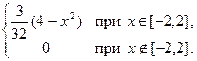

Для нахождения ф.р. F (х) воспользуемся формулой (4.2).

Если х < –2, то р (х) = 0; следовательно,

F (х) =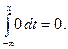

Если –2 £ х £ 2, то р (х) = 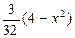; следовательно,

F (х) = 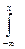р (t) dt =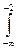0 dt +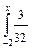(4 – t ²) dt = 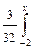(4 – t ²) dt = 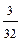(4 t – =

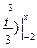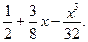
Если х > 2, то р (х) = 0; следовательно,

F (х) =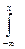 р (t) dt = 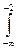0 dt + 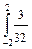(4 – t ²) dt + 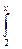0 dt = 1.

Таким образом, искомая функция F (х) имеет вид

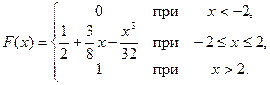
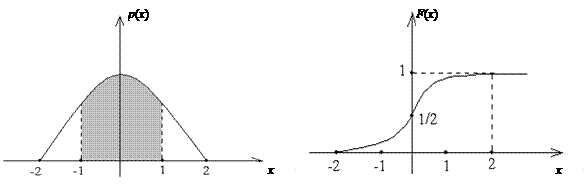Графики функций р (х) и F (х) изображены на рис. 4.2 и 4.3.

Рис. 4.2. Плотность распределения Рис. 4.3. Функция распределения

Подставляя значения х ₁ = –1 и х ₂ = 1 в формулу (4.5), получаем

Р {–1 £ ξ £ 1} = F (1) – F (–1) = 1/2 + 3/8 – 1/32 – (1/2 – 3/8 + 1/32) = 0,75.

На рис. 4.2 заштрихована фигура, площадь которой равна полученной вероятности. ·

Контрольные вопросы

1. Какую случайную величину называют непрерывной?

2. Как задают закон распределения непрерывной случайной величины?

3. Что называют плотностью распределения непрерывной с.в.?

4. Как определяется функция распределения непрерывной с.в.?

5. Сформулируйте характеристические свойства плотности распределения.

6. Чему равна вероятность того, что непрерывная с.в. примет какое-либо определенное значение?

7. Как с помощью плотности распределения p _x(x) вычислить вероятность того, что с.в. x примет значение из промежутка: а) [ a, b ]; б) [ a, b); в) (a, b ]; г) (a, b)?

8. Как на графике плотности распределения p _x(x) изобразить вероятности п.п. а)–г) предыдущего вопроса?

Контрольные задания

1. Является ли плотностью распределения некоторой случайной величины каждая из следующих функций:

а) 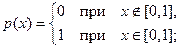б)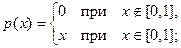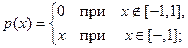

в) в)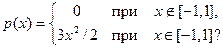

2. Можно ли подобрать постоянную С так, чтобы функция С / x ³ определяла плотность распределения вероятностей на отрезке: а) [1, ¥); б) (0, ¥); в) [–2, 1]?

3. Непрерывная с.в. x имеет плотность распределения:

а)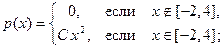

б)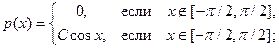

в)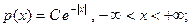

г)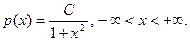

Для каждого распределения необходимо:

1) найти неизвестный параметр С и построить график плотности распределения;

2) найти функцию распределения и построить ее график;

3) вычислить вероятности P {–1 £ x £ 1} и P {x >0}, используя плотность и функцию распределения;
4) проиллюстрировать вероятности п.3) на графике плотности распределения.

4. Функция распределения непрерывной с.в. x имеет вид

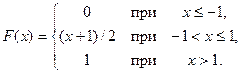
а) Построить график ф.р. F (x).

б) Найти плотность распределения p (x) и построить ее график.

г) Найти вероятности P {xÎ(– 0,5; 1)} и P {0,5 <x < 1} с помощью плотности и функции распределения.

д) Проиллюстрировать вероятности п. г) на графике плотности распределения.

5. Основные непрерывные распределения

1. Равномерное распределение

Случайная величина ξ имеет равномерное распределение на отрезке [ а, b ] (а < b), если ее плотность распределения равна

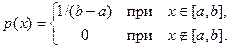
Найдем ф.р. F (х) с.в. ξ. При х Î [ а, b ] по формуле (4.2) имеем

F (х) = =+ = = = .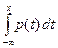

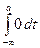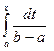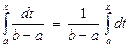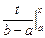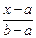Как нетрудно понять (см., например, пример 4.1) при х < а функция F (х) = 0 и F (х) = 1 при х > b.

Таким образом,

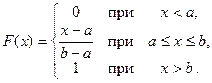
Графики функций р (х) и F (х) приведены на рис. 5.1 и 5.2 соответственно.

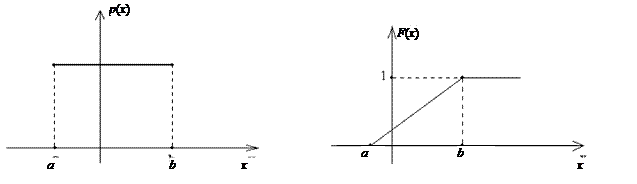Рис. 5.1. Плотность распределения Рис. 5.2. Функция распределения

равномерного закона равномерного закона

Равномерное распределение имеют, например, ошибки округления при проведении числовых расчетов. Такая ошибка, как правило, оказывается равномерно распределенной на интервале от –5 до +5 единиц округляемого десятичного знака. Так, если вычисления проводятся с точностью до 0,001, то ошибка округления при этом равномерно распределена на отрезке [– 0,005; 0,005].

Также равномерное распределение имеет время ожидания «обслуживания» при периодическом, через каждые Т единиц времени, включении (прибытии) «обслуживающего устройства» и при случайном поступлении (прибытии) заявки на обслуживание в этом интервале времени. Например, время ожидания пассажиром прибытия поезда метро при их точных пятиминутных интервалах движения и случайном моменте появления пассажира на платформе будет распределено равномерно на промежутке [0 мин; 5 мин].

Кроме того, равномерное распределение иногда используется в качестве «нулевого приближения» при анализе случайных величин в условиях полного отсутствия априорной информации о законе распределения этой с.в.

2. Показательное (экспоненциальное) распределение

Случайная величина ξ имеет п оказательное (экспоненциальное) распределение с параметром λ (λ > 0), если ее плотность распределения имеет вид

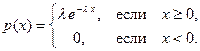
По формуле (4.2) нетрудно получить выражение для ф.р. F (х) данной с.в.:

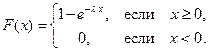
Графики плотности и функции распределения показательно (экспоненциально) распределенной с.в. приведены на рис. 5.3 и 5.4 соответственно.

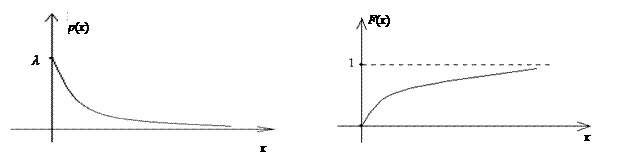Рис. 5.3. Плотность распределения Рис. 5.4. Функция распределения

показательного закона показательного закона

Укажем две области применения теории вероятностей, где показательное распределение играет основную роль.

К первой из них относятся задачи, связанные с величинами типа «времени жизни». Этот термин следует понимать достаточно широко. В медико-биологических исследованиях под ним может подразумеваться продолжительность жизни больных при клинических исследованиях; в технике – продолжительность безотказной работы машин и механизмов; в экономике – продолжительность забастовок или периодов стагнации; в психологии – время, затраченное испытуемым на выполнение тестовых задач и т.д.

Второй областью широкого использования показательного распределения являются задачи массового обслуживания. Здесь речь может идти о любой системе, предназначенной для обслуживания каких-либо заявок (требований), поступающих на нее в случайные моменты времени. Примеры таких систем: телефонная станция; станция «Скорой помощи»; билетная касса; магазин; компьютер и т.д.

3. Нормальное распределение

Случайная величина ξ имеет нормальное распределение с параметрами а и σ (– ¥ < а < + ¥, σ > 0), если ее плотность распределения имеет вид

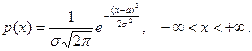
Подчиненность с.в. ξ нормальному закону распределения символически обозначается ξ ~ N (а, σ).

Нетрудно установить (что предоставляется сделать читателю) следующие свойства функции р (х):

· р (х) > 0 для всех х Î R;

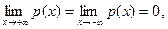· т.е. ось абсцисс является горизонтальной асимптотой для графика функции р (х);

· функция р (х) в точке х = а имеет максимум, равный 1/σ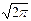≈ 0,4/σ;

· график функции р (х) симметричен относительно прямой х = а;

· функция р (х) имеет перегиб в точках х = а ± σ.

На основании этих свойств построим графики плотностей нормального распределения р (х) (рис. 5.5) для различных значений параметра σ. На рис. 5.5 наглядно показан смысл параметров нормального распределения: параметр а характеризует положение графика функции на числовой прямой, параметр σ характеризует степень сжатия или растяжения графика плотности.

Функция распределения F (x) случайной величины ξ ~ N (а, σ) выражается через функцию Лапласа 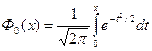по формуле

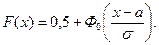(5.1)

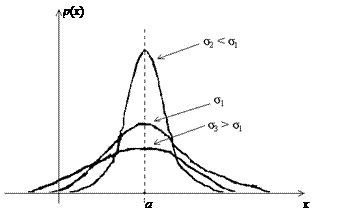
Рис. 5.5. Плотности нормального распределения

Заметим, что функция Лапласа Ф ₀(x) впервые появилась у нас в интегральной теореме Муавра-Лапласа (см. тему 1.2). Там же были рассмотрены ее свойства.

Нормальное распределение с параметрами а = 0 и σ = 1 называется стандартным нормальным распределением. Плотность и функция распределения этого закона обозначаются φ(х) и Ф (х) соответственно и имеют вид

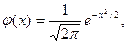
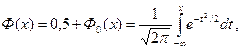(5.2)

– ¥ < x < + ¥.

Поскольку ф.р. F (х) нормального распределения задается выражением (5.1), то в качестве частного случая из теоремы 4.1 вытекает

Теорема 5.1. Если случайная величина ξ ~ N(а, σ), то

1) Р {ξÎ< х ₁, х ₂>} = 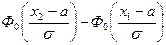(5.3)

для любого интервала < х ₁, х ₂> (замкнутого, открытого, полуоткрытого, ограниченного или неограниченного);

2) Р {|ξ – a| < e}= Р {|ξ – a| £ e} =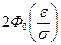 (5.4)

для любого числа e > 0. ¨

Пример 5.1. (правило «трех сигм»). Если с. в. ξ ~ N (а,σ), то практически все значения с.в. ξ находятся в интервале (а – 3σ, а + 3σ):

Р { а – 3σ < ξ < а + 3σ} = 0,9973.

Решение. Воспользовавшись формулой (5.4) для e = 3σ, получаем

Р { а – 3σ < ξ < а + 3σ} = Р {|ξ – a | < 3σ} = 2 Ф ₀(3) = 2×0,49865 = 0,9973. ·

Пример 5.2. Станок-автомат изготавливает шарики для подшипников, номинальный диаметр которых 5 мм. Вследствие неточности изготовления шарика фактический его диаметр представляет собой случайную величину, распределенную по нормальному закону с параметрами а = 5 мм и σ = 0,05 мм. При контроле бракуют все шарики, диаметр которых отличается от номинального больше, чем на 0,1 мм.

1) Какой процент шариков в среднем будет отбракован?

2) Сколько необходимо проверить шариков, чтобы вероятность обнаружения среди них хотя бы одного бракованного была бы не менее 0,95?

Дата добавления: 2014-01-03