
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 1) Пусть ξ – фактический диаметр (в мм) наугад взятого шарика из продукции станка-автомата
|
|
|
|
1) Пусть ξ – фактический диаметр (в мм) наугад взятого шарика из продукции станка-автомата. По условию с.в. ξ ~ N (5; 0,05).
Вероятность события А = {шарик бракуют} = {|ξ – 5| > 0,1} найдем с помощью формулы (5.4) при а = 5, σ = 0,05 и e = 0,1.
Имеем
р = Р (А) = 1 – Р {|ξ – 5| £ 0,1} = 1 – 2 Ф 0(2) = 1 – 2×0,4772 = 0,0456.
Следовательно, в среднем 4,56% продукции станка-автомата будет забраковано.
2) Так как контроль шариков осуществляется, очевидно, независимым образом, а вероятность браковки шарика при каждом испытании постоянна и равна р = 0,0456, то для нахождения необходимого числа n проверок воспользуемся следствием 2.4 из формулы Бернулли (тема 1.2, неравенство (2.6)) при g = 0,95:
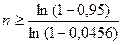 = 64,186.
= 64,186.
Поскольку n – целое число, то n ³ 65. ·
Нормальный закон распределения играет исключительно важную роль в теории вероятностей и ее приложениях и занимает среди других законов особое положение. Нормальное распределение относится к числу наиболее распространенных на практике законов распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма общих предположениях. В качестве непрерывного приближения для биномиального распределения нормальное распределение впервые рассматривалось А. Муавром в 1733 г. (см. локальную и интегральную теоремы Муавра-Лапласа, тема 1.2). Затем нормальное распределение было снова открыто и изучено независимо друг от друга К. Гауссом (1809 г.) и П. Лапласом (1812 г.). Оба ученых пришли к нормальному закону в связи со своей работой по теории ошибок наблюдения.
В теме 1.5, посвященной предельным теоремам, мы увидим, что нормальный закон обычно возникает в явлениях, подверженных действию большого числа малых случайных воздействий. Если некоторая случайная величина представляет собой сумму достаточно большого числа других с.в., то при широких предположениях относительно слагаемых данная с.в. будет подчиняться приближенно нормальному закону распределения.
Контрольные вопросы
1. Какое распределение вероятностей называется равномерным?
2. Какой вид имеет функция распределения F (x) с.в. x, равномерно распределенной на отрезке [ a, b ]?
3. Как определяется показательное (экспоненциальное) распределение с.в.?
4. Какой вид имеет функция распределения для показательного закона?
5. Какое распределение вероятностей называется нормальным?
6. Какими свойствами обладает плотность нормального распределения?
7. Как влияют параметры нормального закона на вид графика плотности нормального распределения?
8. Какой вид имеет функция распределения для нормального закона?
9. Какое распределение называют стандартным нормальным?
10. Как вычислить вероятность попадания значений нормально распределенной с.в. в заданный промежуток?
11. Как вычислить вероятность отклонения значений нормально распределенной с.в. от параметра а?
12. Сформулируйте правило «трех сигм».
Контрольные задания
1. Случайная величина x равномерно распределена на отрезке [–2, 4].
а) Записать плотность распределения с.в. x и построить ее график.
б) Записать функцию распределения с.в. x и построить ее график.
в) Найти вероятности P {| x | £ 1} и P {x > 0}, используя функцию распределения и плотность распределения.
2. Поезда метрополитена идут регулярно с интервалом 5 мин. Пассажир выходит на платформу в случайный момент времени. Рассматривается случайная величина x – время ожидания пассажиром поезда (в мин.).
а) Найти плотность распределения p x(x) и построить ее график.
б) Найти функцию распределения F x(x) и построить ее график.
в) Определить вероятность того, что пассажиру придется ждать поезда не более двух минут с помощью плотности и функции распределения.
3. Установлено, что время ремонта телевизоров (в днях) есть случайная величина x, распределенная по показательному распределению с параметром 0,1.
а) Записать плотность распределения с.в. x и построить ее график.
б) Записать функцию распределения с.в. x и построить ее график.
в) Найти вероятность того, что на ремонт телевизора потребуется не менее 15 дней.
4. Докажите свойства плотности распределения с.в. ξ ~ N (а, σ).
5. Нарисуйте графики плотности и функции распределения с.в. ξ, распределенной по нормальному закону с параметрами а = – 2 и s = 0,2.
6. Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами а = 375 г. и s = 25 г. Определить вероятность того, что вес одной наудачу взятой рыбы будет: а) от 300 до 425 г.; б) не более 450 г.; г) больше 300 г.
7. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с параметром s = 10 мм. Найти вероятность того, что измерение произведено с ошибкой, не превосходящей 15 мм.
8. Автомат изготавливает подшипники, которые считаются годными, если отклонение x от проектного размера по модулю не превышает 0,7 мм. Каково наивероятнейшее число годных подшипников среди 100 изготовленных, если с.в. x распределена нормально с параметром s = 0,4 мм? Определить вероятность такого числа годных подшипников среди 100 изготовленных.
6. Многомерные случайные величины. Независимость случайных величин
САМОСТОЯТЕЛЬНО!!!
Во многих ситуациях результат испытания характеризуется не одной случайной величиной, а некоторой совокупностью случайных величин x1, x2, …, x n, которую называют также многомерной (n - мерной) случайной величиной 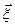 = (x1, x2, …, x n). При этом x i называют i -й компонентой
= (x1, x2, …, x n). При этом x i называют i -й компонентой 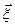 .
.
Приведем примеры многомерных случайных величин.
1. Успеваемость выпускника вуза характеризуется совокупностью n случайных величин x1, x2, …, x n – оценками по различным дисциплинам, проставленными в приложении к диплому.
2. Погода в данной местности в определенное время суток может быть охарактеризована совокупностью случайных величин: x1 – температура; x2 – давление; x3 – скорость ветра; x4 – влажность и т. п.
Случайные величины x1, x2, …, x n, входящие в совокупность, могут быть дискретными (см. выше пример 1), непрерывными (пример 2), смешанными (дискретно-непрерывными).
Наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения, который в общем виде дается ее функцией распределения.
Функцией распределения n-мерной случайной величины 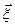 = (x1, x2, …, x n) называется функция n аргументов
= (x1, x2, …, x n) называется функция n аргументов 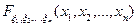 , выражающая вероятность совместного осуществления (пересечения) n событий {x1 < x 1}, {x2 < x 2},…, {x n < xn }:
, выражающая вероятность совместного осуществления (пересечения) n событий {x1 < x 1}, {x2 < x 2},…, {x n < xn }:
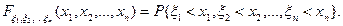 (6.1)
(6.1)
Многомерную функцию распределения называют также совместной функцией распределения случайных величин x1, x2, …, x n.
В двумерном случае для совокупности случайных величин (x, h) совместная функция распределения 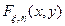 определяется равенством
определяется равенством


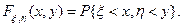 (6.2)
(6.2)
Двумерная с.в., или двумерная совокупность с.в. (ξ, η), называется дискретной, если каждая из с.в. ξ и η является дискретной.
Так же, как и в одномерном случае, распределение дискретной двумерной с.в. естественно описать с помощью перечисления всевозможных пар (хi, уj) значений двумерной с.в. (ξ, η) и соответствующих вероятностей рij, с которыми эти пары значений принимаются с.в. ξ и η:
рi j = Р {ξ = хi, η = уj }, i = 1, 2, …; j = 1, 2, … (6.3)
Исходя из двумерного закона распределения (6.3) дискретной случайной совокупности (ξ, η), нетрудно получить распределения его компонент:
рi ▪ = Р {ξ = хi } = 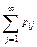 , i = 1, 2,….
, i = 1, 2,….
р ▪ j = Р {η = уj } = 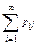 , j = 1, 2, ….
, j = 1, 2, ….
 |
Заметим также, что
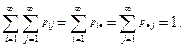
Двумерная с.в., или двумерная совокупность с.в. (ξ, η), называется непрерывной, если ее компоненты ξ и η непрерывны. Для двумерной с.в. (ξ, η) ее функция распределения F ξ,η(х, у) непрерывна и дифференцируема по своим аргументам.
Распределение двумерной с.в. (ξ, η) можно задавать, наряду с совместной ф.р. F ξ,η(х, у), также двумерной или совместной плотностью распределения 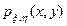 , равной второй смешанной производной ф.р. F ξ,η(х, у):
, равной второй смешанной производной ф.р. F ξ,η(х, у):
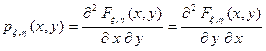 . (6.4)
. (6.4)
Исходя из двумерного закона распределения (6.4) непрерывной двумерной с.в. (ξ, η) можно получить распределения его компонент:
р ξ(х) = 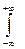 р ξ, η (х, у) dy, – ¥ < x < + ¥;
р ξ, η (х, у) dy, – ¥ < x < + ¥;
р η(y) = 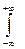 р ξ, η (х, у) dx, – ¥ < y < + ¥.
р ξ, η (х, у) dx, – ¥ < y < + ¥.
Введем очень важное для приложений понятие независимости случайных величин.
Случайные величины ξ1, ξ2, …, ξ n называются независимыми (в совокупности или взаимно), если их совместная функция распределения представляется в виде произведения одномерных функций распределения:
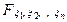 (х 1, х 2, …, хn) =
(х 1, х 2, …, хn) = 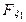 (х 1)
(х 1) 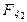 (х 2)…
(х 2)… 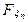 (хn).
(хn).
Независимость с.в. ξ1, ξ2, …, ξ n означает, что совместный закон распределения совокупности с.в. представим в виде произведения законов распределения компонент этой совокупности.
Случайные величины ξ1, ξ2, …, ξ n называются попарно независимыми, если любая пара из них независима. Так же, как и для событий, из попарной независимости с.в. не следует независимость с.в. в совокупности.
Для проверки независимости компонент многомерных дискретных и непрерывных случайных векторов обычно бывают более удобными другие эквивалентные определения независимости, которые мы приведем для двумерного случая.
Дискретные с.в. ξ и η независимы, если для всех i, j = 1, 2, ….
рi j = рi ▪· р ▪ j, т.е. Р {ξ = хi, η = уj }= Р {ξ = хi } Р {η = уj }.
Непрерывные с.в. ξ и η независимы, если для всех х, у Î R
р ξ,, η (х, у) = р ξ(x) р η(у).
Понятие независимости случайных величин ξ и η представляет собой перенос понятия независимости событий на с.в. и отражает отсутствие связи между с.в. ξ и η. Иными словами, независимость с.в. ξ и η можно охарактеризовать следующим образом: зная значение, которое приняла с.в. η, мы никакой новой информации о распределении с.в. ξ не получим.
Контрольные вопросы
1. Какую случайную величину называют: а) двумерной; б) трехмерной; в) n -мерной?
2. Как задается закон распределения многомерной случайной величины?
3. Дайте определение совместной функции распределения совокупности с.в., состоящей: а) из двух с.в.; б) трех с.в.; в) n с.в.
4. Какая многомерная случайная величина называется дискретной?
5. Как можно задать закон распределения двумерной дискретной с.в.?
6. Как, зная закон распределения двумерной дискретной с.в., найти законы распределения ее компонент?
7. Какая многомерная случайная величина называется непрерывной?
8. Как можно задать закон распределения двумерной непрерывной с.в.?
9. Как, зная закон распределения двумерной непрерывной с.в., найти законы распределения ее компонент?
10. Как определяется независимость совокупности случайных величин?
11. Как определяется независимость двух с.в.: а) дискретных; б) непрерывных?
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 6; гл. 10–11; гл. 12, п.п. 1–7; гл. 13, п.п. 1–2, 4–6; гл. 14, п. 16.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 4, п.п. 1–2; гл. 6, п.п. 1–2, 4–7; гл. 8.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 713; Нарушение авторских прав?; Мы поможем в написании вашей работы!