
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Главная формула RM
|
|
|
|
С самого начала пятидесятых годов Г.Раша привлекли к оценке интеллектуальных способностей призывников датской армии. Он сразу же обратил внимание на основной недостаток применявшихся тогда психологами тестов, в которых были только задания с выбором одного правильного ответа. У этих заданий есть существенный дефект - высокая вероятность угадывания правильного ответа теми испытуемыми, кто не обладал интеллектуальными способностями. Поэтому первое, что он сделал – решительно отказался от таких заданий и перешёл к применению заданий открытой формы. Другие формы заданий в то время не были достаточно известны.
Модель Раша опирается на понятия "трудность задания" и "уровень подготовленности". Так, одно задание считается более трудным, чем другое, если вероятность правильного ответа на первое задание меньше, чем на второе, независимо от того, кто их выполняет. Аналогично, более подготовленный студент имеет большую вероятность правильно ответить на все задания, чем менее подготовленный.
Благодаря простой структуре модели существуют удобные вычислительные процедуры для проверки адекватности модели: для всего набора тестовых результатов, для каждого испытуемого, для каждого задания и для каждого конкретного ответа.
Рассмотрим модель Раша более подробно. Пусть тест состоит из К различных заданий бинарного типа), испытуемый получает 1, если ответил правильно и 0 при неверном ответе) и его выполняют N – студентов. В результате получается матрица ответов An,k состоящая из N- строк (i) и К –столбцов (j).
Число bi равное сумме баллов в i- строке называется первичным баллом i- испытуемого (оно равно числу его правильных ответов):
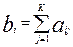
При необходимости первичный балл можно выразить в процентах (или долях). Уровни подготовленности участников A и B обозначим через SА и SВ, а трудность заданий через t (на самом деле все задания имеют разный уровень трудности tk). В модели Раша доказывается, что:
 (1)
(1)

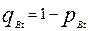 ,
,
где 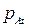 и
и 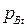 - вероятность выполнения задания уровня трудности t соответственно участниками A и B,
- вероятность выполнения задания уровня трудности t соответственно участниками A и B, 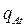 и
и 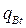 - вероятности невыполнения задания уровня трудности t соответственно участниками A и B. Из общих соображений выражение (1) должно быть верным для любого уровня трудности заданий и любой пары участников тестирования. Пусть, какое либо задание имеет трудность t=1 и необходимо сравнить трудности двух заданий. В модели Раша уровень трудности определяется, как отношение вероятности (
- вероятности невыполнения задания уровня трудности t соответственно участниками A и B. Из общих соображений выражение (1) должно быть верным для любого уровня трудности заданий и любой пары участников тестирования. Пусть, какое либо задание имеет трудность t=1 и необходимо сравнить трудности двух заданий. В модели Раша уровень трудности определяется, как отношение вероятности (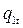 ) того, что некоторый стандартный участник испытания с единичным уровнем подготовки (S=1) не выполнит данное задание к вероятности (
) того, что некоторый стандартный участник испытания с единичным уровнем подготовки (S=1) не выполнит данное задание к вероятности ( ) его выполнения:
) его выполнения:
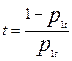 .
.
Единичный уровень подготовки и единичная трудность задания в модели Раша связаны между собой. Используя выражение:
 ,
,
и предположив, что уровень подготовленности именно участника В является единичным (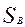 =1) получим следующее выражение:
=1) получим следующее выражение:
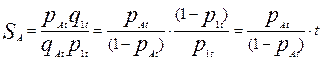 (2)
(2)
Уравнение (2) связывает уровень трудности некоторого задания и уровень подготовленности некоторого участника с вероятностью правильного выполнения задания и должно быть справедливо для заданий любого уровня трудности. Учитывая общность полученного уравнения (2) можно показать, что вероятность Р(S,t), того, что участник с уровнем подготовки S правильно выполнит задание трудности t, выражается следующей формулой:
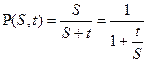 (3)
(3)
Вероятность Р(S,t) получила название функции успеха. Как видно из выражения (3) функция успеха зависит только от отношения t к S, поэтому модель Раша называется однопараметрической и использует шкалу отношений.
Вводя новые переменные:
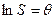 ,
,  ,
,
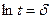 ,
, 
Выражение (3) можно переписать в виде:
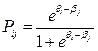 или
или 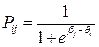 (4)
(4)
Формула (4) является основным уравнением однопараметрической логистической модели Раша, единица измерения δ и θ называется логитом. При одном логите (δ0=1 и θ0=1) вероятность успеха 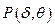 =0,5, т.е. вероятность выполнения стандартного задания стандартным участником должна быть равна 0,5 (см. рис.1). Модель Раша позволяет сделать один очень важный вывод: чем выше уровень подготовки участника, тем больше вероятность выполнения задания любого уровня трудности. Стоит отметить, что параметры δ и θ называют латентными параметрами, т.к. они не измеряются непосредственно в процессе тестирования.
=0,5, т.е. вероятность выполнения стандартного задания стандартным участником должна быть равна 0,5 (см. рис.1). Модель Раша позволяет сделать один очень важный вывод: чем выше уровень подготовки участника, тем больше вероятность выполнения задания любого уровня трудности. Стоит отметить, что параметры δ и θ называют латентными параметрами, т.к. они не измеряются непосредственно в процессе тестирования.
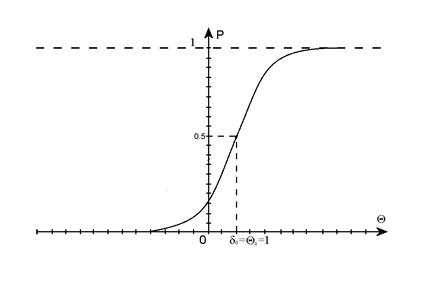
Рис.1. Характеристическая кривая трудности задания
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1047; Нарушение авторских прав?; Мы поможем в написании вашей работы!