
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие числового ряда. Сходимость числового ряда
|
|
|
|
Лекция 7. Числовые и функциональные ряды.



Главным критерием сходимости ряда является критерий Коши.

Исследование рядов на сходимость значительно облегчается, если известно, что все члены ряда сохраняют знак. Без ограничения общности можно считать, что они положительны.

Для знакочередующихся рядов ситуация сложнее. Но и для них есть достаточные условия (признаки) сходимости.

Этот признак сходимости называется признаком Лейбница.

Для знакопеременных рядов вводится понятие абсолютной и условной сходимости.


Теперь рассмотрим функциональные последовательности и ряды.
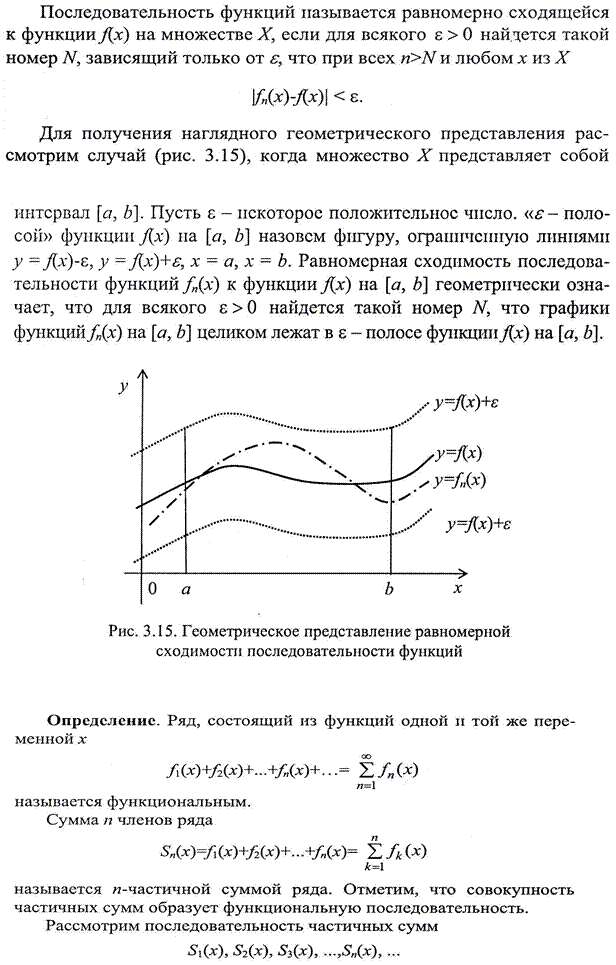 |


Перейдем теперь к рассмотрению степенных рядов.




|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1551; Нарушение авторских прав?; Мы поможем в написании вашей работы!