Распределение скорости в заснарядном пространстве

При изучении движения продуктов горения в канале ствола орудия рассматривает одномерный квазистационарный поток. Для определения параметров потока в произвольной точке заснарядного пространства плотности r_Г, температуры Т_Г, и скорости w_Г необходимо воспользоваться системой уравнений газодинамики, включающей уравнение состояния и уравнение сохранения вещества, количества движения и энергии.

Обычно во внутренней баллистике делают следующие допущения:

1. плотность продуктов горения одинакова во всех точках заснарядного пространства;

2. канал ствола орудия представляет собой цилиндр (уширением каморы пренебрегают);

3. трение продуктов горения о стенки ствола отсутствует;

4. продукты горения имеют только поступательное движение.

Очевидно, все параметры потока будут одинаковыми в любой точке данного поперечного сечения канала.

Обозначим через L = l₀ + l расстояние от дна канала ствола до дна снаряда, а через х_Г - расстояние от дна канала ствола до рассматриваемого сечения. Воспользуемся уравнением сохранения вещества

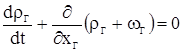(2.1)

В соответствии с первым допущением можем записать

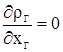
и тогда уравнение 2.1 получит вид

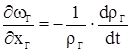
Интегрируя это уравнение для заданного момента времени t по w_Г от нуля до w_Г, а по х_Г oт нуля до х_Г, получим

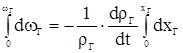
или

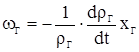(2.2)

Результатом волнообразного движения продуктов горения может быть волнообразное изменение давления пороховых газов в заснарядном пространстве и выскоки давления за допустимые пределы. Задача о распределении плотности, скорости и давления в канале ствола носит название задачи Лагранжа.

В классической внутренней баллистике волнообразным характером движения продуктов горения пренебрегают.

Средняя плотность продуктов горения в заснарядном пространстве равна

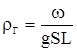, (2.3)

откуда найдем

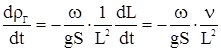
подставляя в равенство 2.2 выражения для r_Г и 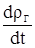, находим

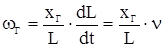. (2.4)

Из выражения 2.4 следует, что в каждый момент времени скорость продуктов горения при сделанных допущениях изменяется в заснарядном пространстве линейно от нуля у дна, канала ствола до величины скорости снаряда V у дна снаряда.

Количество движения М_Г истока продуктов горения будет равно

,

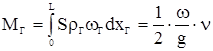а его кинетическая энергия Е_Г равна

.

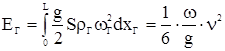Если учесть уширение каморы, то в формулах необходимо взять вместо величины w меньшую величину w' продуктов горения, находящихся в движении. Принимаем по предложению проф. В. Е. Слухоцкого

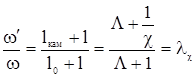(2.5)

где 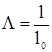- относительный путь снаряда,

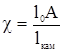- коэффициент уширения каморы. В результате получим уточненные формулы

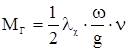(2.6)

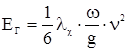(2.7)

Очевидно, что множитель l_c всегда будет меньше единицы и является величиной переменной. В расчетах величина l_c берется средним значением на участке от 0 до L_m при определении p_max на участке от 0 до L_д при определении V_д.

Дата добавления: 2014-01-03