Распределение давлений в заснарядном пространстве

Уравнение сохранения количества движения потока

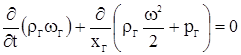(3.1)

после допущения о постоянстве плотности продуктов горения тоже упростится, так как на основании равенства 2.4 можно записать

;

;

.

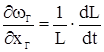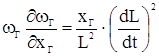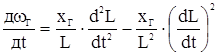Уравнение 3.1 сначала запишем в виде

,

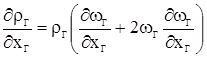а затем, подставляя полученные выше соотношения, получим

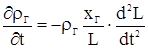
Для заданного момента времени это уравнение относительно переменных р_Г и х_Г является линейным уравнением первого порядка. Его решение можно записать следующим образом:

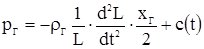, (3.2)

где c(t) - произвольная функция, определяемая по граничным ус­ловиям: при х_Г=L, р_Г = р_cm. Получаем из уравнения 3.2

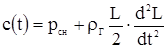
и, имея в виду, что 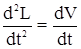, перепишем равенство

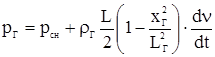(3.3)

Учитывая уравнение поступательного движения 1.7 из лекции № 6, выражение для r_Г 2.3 и уширение каморы, получим соотношение между давлениями пороховых газов в любом сечении и у дна снаряда:

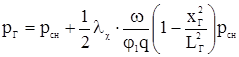(3.4)

где обозначено

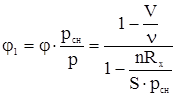(3.5)

Как видим из равенства 3.4, давление пороховых газов в заснарядном пространстве увеличивается по параболической зависимости от величины р_сн у дна снаряда до величины р_кн дна канала ствола.

При х_Г = 0 получим величину р_кн:

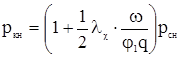, (3.6)

откуда, найдем

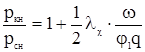(3.7)

Видим, что разница между величинами р_кн и р_сн будет тем большей, чем больше будет относительный вес порохового заряда 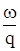. Отношение этих величин практически постоянно при движении снаряда (l_c = const).

Если осредним по длине заснарядного пространства давление пороховых газов р_Г, то получи величину баллистического давления р

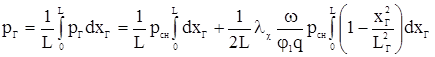
или

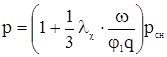(3.8)

Отсюда, найдём

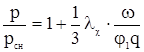(3.9)

Как видим, отношение между баллистическим давлением и давлением у дна снаряда остается практически постоянным во все время движения снаряда в канале ствола.

Дата добавления: 2014-01-03