ЛЕКЦИЯ № 8

Механические волны. Элементы акустики.

План

1. Волны. Поперечные и продольные волны.

2. Волновое число. Связь между скоростью и длиной волны.

3. Принцип Гюйгенса.

4. Уравнение бегущей волны. Фазовая скорость.

5. Энергия волны. Объемная плотность энергии. Плотность потока энергии. Вектор Умова.

6. Стоячие волны.

1.

Процесс распространения колебаний в упругой среде называется волной.

Частицы среды, в которой волна распространяется, не движутся вместе с волной, а колеблются около некоторого положения равновесия.

Основным свойством всех волн является перенос энергии без переноса вещества.

Волны бывают: упругими, волна на поверхности жидкости и электромагнитными.

Упругие или механические волны это колебания, распространяющиеся в упругой среде.

Они бывают продольными и поперечными.

Если частицы среды колеблются в направлении перпендикулярном направлению распространения волны, то волна называется поперечной.

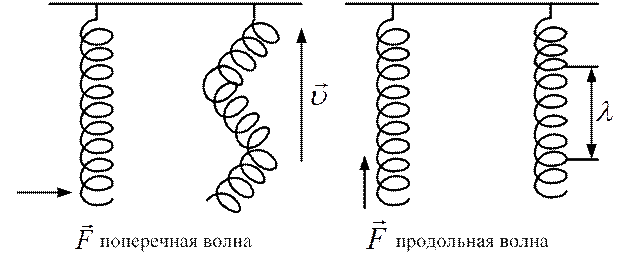
В продольной волне направление колебания частиц совпадает с направлением распространения волны.

λ – лямбда – длина волны, расстояние между центрами двух ближайших сгущений или растяжений.

2.

Продольные волны – в средах, где деформация растяжения или сжатия (жидкость, газ, твердое тело).

Поперечные волны – при деформации сдвига, т. е. только в твердых телах.

Упругая волна называется синусоидальной или гармонической, если соответствующие колебания частиц среды являются гармоническими. Гармоническая волна может быть изображена синусоидой.

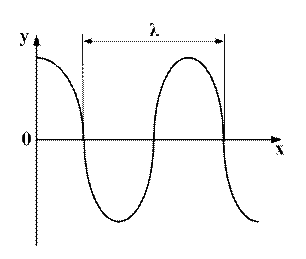
λ – длина волны, расстояние между двумя ближайшими точками колеблющимися в одной фазе.

0 – источник колебания.

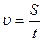, t = T, S = λ

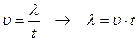(1)

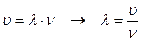(2)

Для характеристики волны вводят понятие волновое число 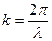, подставим в формулу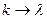

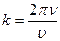, но 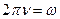- циклическая частота.

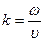- волновое число.

.

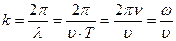3.

Пусть некоторая точка колеблется в сплошной упругой однородной среде. Тогда колебания от этой точки будут распространяться во все стороны.

Геометрическое место точек, до которых к данному моменту дошли колебания, называется фронтом волны.

Если источник колебаний точечный и колебания распространяются в однородной среде, то фронт волны будет сферой и волна называется сферической.

Если фронт волны плоский, то волна называется плоской.

Голландский физик Гюйгенс в конце XVII века дал способ построения нового фронта волны, если известно положение его в некоторый предыдущий момент.

Принцип Гюйгенса: каждая точка фронта волны является источником элементарных вторичных волн. Огибающая всех этих элементарных волн представляет собой новый фронт волны.

1 – фронт волны в некоторый момент времени t/

За промежуток времени Δt от каждой точки фронта волны распространяется 2 – новый фронт волны.

4.

Уравнение бегущей волны. Фазовая скорость.

Бегущей называется волна, уносящая в пространство энергию.

Выведем уравнение бегущей волны.

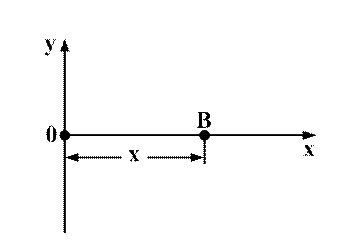
Пусть точка 0 совершает гармонические колебания

y = A·cosωt.

В точке В на оси х колебания будут проходить по тому же закону, но будут отставать по времени на 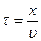, где 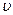- скорость распространения волны (в однородной среде 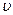= const) и уравнение колебания частиц в точке В примет вид

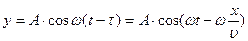, но

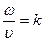- волновое число.

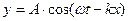- уравнение бегущей волны.

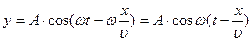-уравнение плоской волны.

Если волна распространяется в противоположном направлении в сторону убывания то .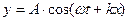

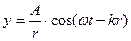- уравнение сферической волны, где r – расстояние от источника до рассматриваемой точки.

Предположим, что фаза в уравнении бегущей волны есть величина постоянная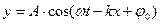

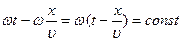
Продифференцируем выражение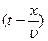

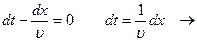
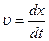- фазовая скорость.

Скорость перемещения волны это есть скорость перемещения фазы, поэтому эта скорость называется фазовой скоростью.

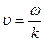- фазовая скорость зависит от частоты, это явление получило название дисперсия волн, а среда в которой волнв распространяются диспергирующей средой.

Скорость распространения волны зависит от свойств среды 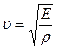, Е – модуль Юнга, 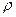- плотность среды.

5.

Энергия волны. Объемная плотность энергии. Плотность потока энергии. Вектор Умова.

Пусть плоская синусоидальная волна 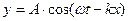распространяется в декартовой системе координат.

Выделим элементарный объем среды dV = dx·dy·dz = dx·dS, массой dm. Этот элементарный объем dV находится в волновом движении и обладает полной энергией складывающейся из dE_k (кинетическая) и dE_n (потенциальная) и полная энергия ,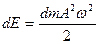

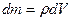
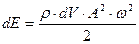- полная энергия волны объема dV.

Объемная плотность энергии W.

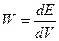- объемная плотность энергии (энергия единичного объема).

.

dФ – поток энергии.

Дата добавления: 2014-01-03