
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие монотонной функции. Признаки монотонности
|
|
|
|
Лекция № 8
Тема: «Монотонность и экстремум функции»
| 1. Признаки монотонности 2. Максимум и минимум функции. Необходимое условие экстремума 3. Достаточное условие экстремума. Первое правило исследования на экстремум 4. Второе правило исследования на экстремум 5. Наибольшее и наименьшее значения функции на отрезке |
Рассмотрим монотонность функции и исследуем её с помощью первой производной. Предварительно вспомним определение возрастающей и убывающей функции.
| О.1.1 | Функция 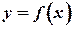 , определенная на сегменте (интервале)
называется возрастающей на этом интервале, если из неравенства , определенная на сегменте (интервале)
называется возрастающей на этом интервале, если из неравенства 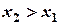 , где , где 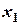 и и 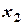 - любые две точки интервала, следует неравенство - любые две точки интервала, следует неравенство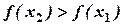 . (Большим значениям независимой переменной, соответствует большее значение функции). . (Большим значениям независимой переменной, соответствует большее значение функции).
|
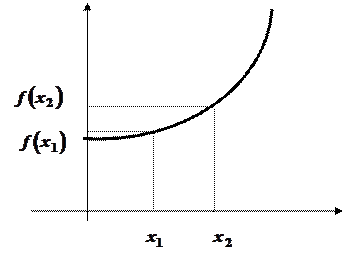 |
Введя обозначения 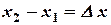 и
и 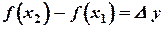 , заметим, что
, заметим, что 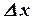 и
и 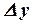 имеют одинаковые знаки. Следовательно, для возрастающей функции отношение приращений функции и аргумента всегда положительно
имеют одинаковые знаки. Следовательно, для возрастающей функции отношение приращений функции и аргумента всегда положительно 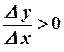 ,
,
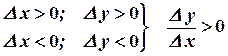
 (1)
(1)
(для возрастающей функции).
О.1.2.Функция 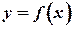 , определенная на сегмента (интервале) называется убывающей на этом интервале, если из
, определенная на сегмента (интервале) называется убывающей на этом интервале, если из
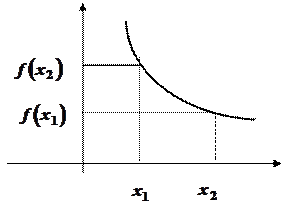 |
неравенства
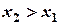 ,
, 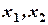 принадлежат сегменту, следует,
принадлежат сегменту, следует,
что 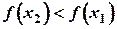 .
.
В этом случае 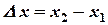 и
и 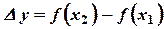 имеют разные знаки, поэтому
имеют разные знаки, поэтому
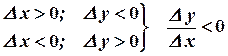 . (2)
. (2)
(для убывающей функции).
Установим необходимые и достаточные условия возрастания и убывания функции в интервале.
| Т. 1.1. | (Необходимое условие возрастания функции). Если дифференцируемая в интервале 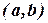 функция функция 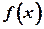 возрастает, то её производная не может быть отрицательной ни в одной точке этого интервала, т.е. возрастает, то её производная не может быть отрицательной ни в одной точке этого интервала, т.е. 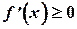 для для 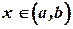 . .
|
Доказательство
Пусть 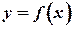 - возрастает на
- возрастает на 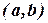 . Рассмотрим две точки
. Рассмотрим две точки 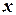 и
и 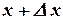 из
из 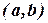 ,
, 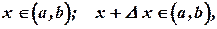
Тогда на основании (1) 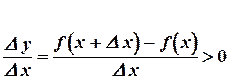 .
.
Переходя к пределу при 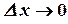 , получим (на основании свойства функции, имеющей конечный предел в точке)
, получим (на основании свойства функции, имеющей конечный предел в точке) 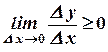 . Т.к. функция по предположению дифференцируема, то
. Т.к. функция по предположению дифференцируема, то 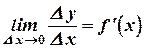 и, следовательно
и, следовательно 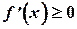 .
.
| Т.1.2. | (Необходимое условие убывания функции). Если дифференцируемая на интервале 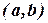 функция функция 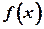 убывает, то её производная не может быть положительна ни в одной точке данного интервала т.е. убывает, то её производная не может быть положительна ни в одной точке данного интервала т.е. 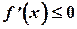 , для , для 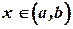 . .
|
Доказательство аналогично.
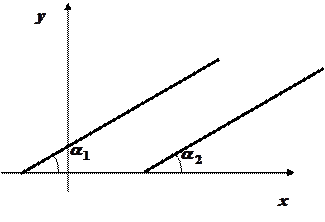 |
Рассмотрим геометрический смысл этих теорем. График возрастающей функции при движении вправо по оси абсцисс поднимается вверх. Касательные к графику функции образуют с
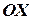 - острые углы.
- острые углы.
Или в некоторой точке касательная может быть параллельна оси 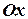 Тангенсы острых углов положительны, и учитывая, геометрический смысл производной
Тангенсы острых углов положительны, и учитывая, геометрический смысл производной 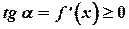 .
.
Аналогично, для функции убывающей, касательные образуют с положительным направлением оси 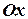 тупые углы. Так как тангенсы тупых углов отрицательны, то
тупые углы. Так как тангенсы тупых углов отрицательны, то 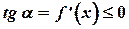 .
.
 |
| Т.1.3. | Достаточное условие возрастания функции. Если непрерывная на интервале 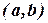 , функция , функция 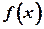 имеет в любой внутренней точке этого интервала положительную производную, то эта функция возрастает на имеет в любой внутренней точке этого интервала положительную производную, то эта функция возрастает на 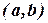 . .
|
Доказательство
Пусть 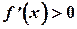 для всех
для всех 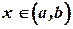 . Рассмотрим два произвольных
. Рассмотрим два произвольных 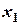 и
и 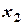 из
из 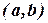 , причем
, причем 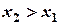 . Напишем формулу Лагранжа применительно к сегменту
. Напишем формулу Лагранжа применительно к сегменту 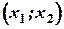 , получим
, получим
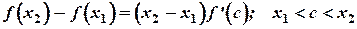 .
.
Во всех точках 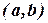 ,
, 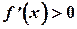 , поэтому и
, поэтому и 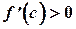 . Так как, кроме того
. Так как, кроме того 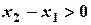 , то
, то 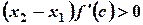 . Следовательно, и левая часть
. Следовательно, и левая часть 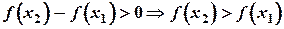 , т.е. функция возрастает на
, т.е. функция возрастает на 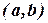 .
.
| Т.1.4. | Достаточное условие убывания функции. Если непрерывная на интервале 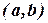 функция функция 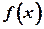 в каждой внутренней точке этого интервала имеет отрицательную производную, то эта функция убывает на в каждой внутренней точке этого интервала имеет отрицательную производную, то эта функция убывает на 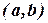 . .
|
Пример.
1) 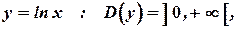
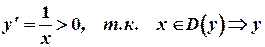 - возрастающая функция.
- возрастающая функция.
2) 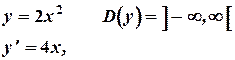
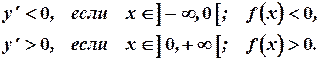
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1203; Нарушение авторских прав?; Мы поможем в написании вашей работы!