Лекция 8. Расчет показателей разработки слоистого пласта на основе модели поршневого вытеснения нефти водой

Показатели, близкие к реальным, получают в ряде случаев при расчете разработки нефтяных месторождений с помощью модели, состоящей из моделей процесса поршневого вытеснения нефти водой и слоистого пласта.

Прежде всего рассмотрим процесс поршневого вытеснения нефти водой из одного прямолинейного слоя (пропластка) толщиной 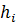и длиной l, пористостью 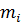и проницаемостью 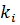(рис. 1).

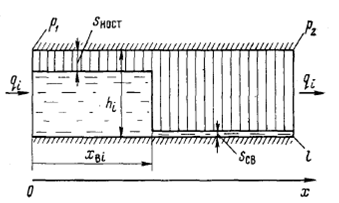
Рис. 1. Модель прямолинейного пропластка при поршневом вытеснении нефти водой

Пусть давление воды, входящей слева в пропласток, равно 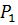, а давление воды на выходе из него 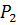. Будем считать, что в течение всего процесса вытеснения нефти водой из слоя перепад давления 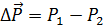постоянный. В соответствии с моделью поршневого вытеснения нефти водой остаточная нефтенасыщенность в заводненной области слоя остается постоянной, равной 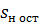. Согласно рис. 1, фронт вытеснения занимает в момент времени t положение 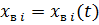. Ширина пропластка, измеряемая в направлении, перпендикулярном к плоскости чертежа (см. рис. 1), равная ширине всего пласта, составляет b. При постоянном перепаде давления на входе в пропласток и на выходе из него расход закачиваемой воды 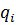будет изменяться со временем.

Предположим, что в заводненной зоне, т. е. при 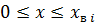, связанная вода с начальной насыщенностью 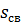полностью смешивается с закачиваемой водой, так что условно (см. рис. 1) заводненная область насыщена остаточной нефтью и этой смесью. Тогда суммарный объем воды 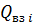, вошедший в область пропластка при 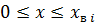, можно определить по формуле:

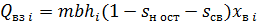(1)

Дифференцируя это выражение по времени t, получим следующую формулу для расхода воды, поступающей в i-й пропласток:

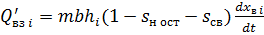(2)

С другой стороны, можно, согласно обобщенному закону Дарси, т. е. с учетом того, что фазовые проницаемости для воды и нефти соответственно составляют 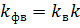, 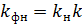(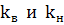- постоянные относительные проницаемости), получить для расхода воды следующее выражение:

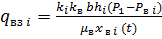(3)

где 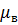— вязкость воды.

При рассмотрении процессов вытеснения нефти водой принимают, что нефть и вода — несжимаемые жидкости. Сжимаемость пород пласта также не учитывают. Поэтому, аналогично формуле (3),можно написать для дебита нефти, получаемой из того же i- го пропластка, выражение:

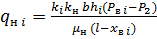(4)

где 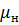— вязкость нефти.

Из выражений (3) и (4), исключая из них давление 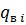- на фронте вытеснения, получим

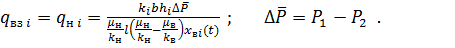(5)

Приравнивая (2) и (5), получим следующее дифференциальное уравнение относительно 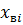(t):

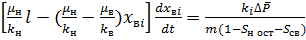. (6)

Интегрируя (6) и учитывая, что 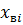= 0 при t = 0, приходим к следующему квадратному уравнению относительно .

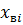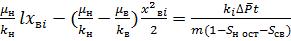(7)

Решая это квадратное уравнение, получаем окончательные формулы для определения 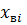в пропластке с проницаемостью k в любой момент времени:

;

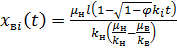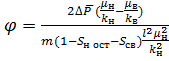(8)

Для того чтобы получить формулу для определения времени 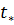,обводнения i- гo пропластка с проницаемостью 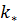, положим в первой формуле (8) .

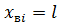Тогда

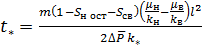; (9)

Из формулы (9) следует, что пропласток с очень большой проницаемостью обводнится в самом начале процесса вытеснения нефти водой из слоистого пласта.

Рассмотрим процесс вытеснения нефти водой из слоистого пласта. Для удобства сложим мысленно все пропластки этого пласта в один “штабель”, причем таким образом, чтобы абсолютная проницаемость пропластков изменялась последовательно, начиная с наименьшей и кончая самой высокой.

Пусть, например, в нижней части этого “штабеля” расположен пропласток с самой большой проницаемостью, а вверху -с наименьшей проницаемостью. Согласно вероятностно -статиcтической модели слоисто-неоднородного пласта, суммарную толщину 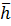пропластков, проницаемость самого проницаемого из которых не ниже, чем некоторое значение, равное k, можно установить в соответствии с формулой закона распределения проницаемости следующим образом:

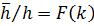(10)

где h - общая толщина всех пропластков в “штабеле”.

Формулу (10) можно представить в дифференциальном виде, т. е. через плотность распределения, следующим образом:

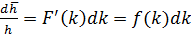(11)

Здесь f(k) — плотность вероятностно-статистического распределения абсолютной проницаемости.

Вытеснение нефти водой из слоистого пласта в целом можно рассматривать и иным образом, считая, что в некоторые слои толщиной 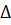h и проницаемостью k поступает вода с расходом 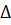q. Тогда из формул (5) и (8)

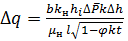(12)

С учетом (11) из (12), заменяя конечные приращения соответствующих величин их дифференциалами и опуская индекс i, найдем:

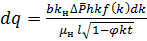(13)

Согласно модели поршневого вытеснения, из обводнившихся пропластков нефть не извлекается — из них поступает только вода. Обводняются, конечно, в первую очередь высокопроницаемые пропластки. В используемых в теории разработки нефтяных месторождений моделях пластов условно принимают, что в слоисто-неоднородных пластах могут быть слои с бесконечно большой проницаемостью. Таким образом, к моменту времени 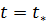когда обводнятся все слои с проницаемостью 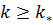, можно добывать нефть лишь из слоев с проницаемостью 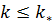. В соответствии со сказанным для дебита нефти из рассматриваемого слоистого пласта на основе (13) получим следующее выражение:

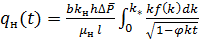(14)

Дебит воды 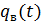можно определить также с учетом указанных соображений по формуле:

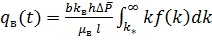(15)

С помощью приведенных формул можно, задаваясь последовательно значениями времени 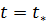, пo (9) определять 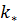. Затем, предполагая, что плотность вероятностно-статистического распределения абсолютной проницаемости известна,можно определить, проинтегрировав (14) и (15), 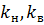и .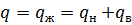

Приведенные выкладки и формулы пригодны, как уже было указано, для случаев, когда в течение всего процесса вытеснения нефти водой из слоистого пласта перепад давления не изменяется. Когда же задано условие постоянства расхода 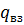закачиваемой в слоистый пласт воды, получают несколько иные соотношения для определения дебитов нефти и воды, а также перепада давления, который в данном случае будет изменяться с течением времени. Если 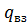= const, справедливы формулы (5) и (6), следует при этом учитывать, что перепад давления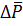-функция времени, т. е. ( .

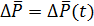Введем функцию :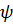

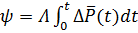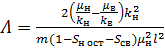; . (16)

Из формулы (5), если ее записать относительно дифференциалов расхода q и толщины пласта h, с учетом (16) получим:

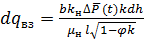(17)

Как и в случае постоянного перепада давления, припостоянном расходе закачиваемой в слоистый пласт воды к некоторому моменту времени 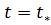часть слоев окажется полностью обводненной и из них будет добываться только вода, из другой же части будут добывать безводную нефть. Поэтому полный расход закачиваемой во всю толщу слоистого пласта воды 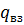можно определить в результате интегрирования выражения (17) и прибавления к правой его части интеграла, учитывающего приток воды из обводнившихся слоев. Имеем:

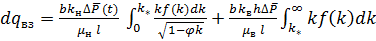(18)

Обучающемуся предлагается следующая процедура последовательного определения 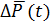. Вначале следует задаться значением проницаемости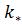, по формуле (9) определить время обводнения слоя 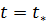, после чего для данного 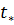вычислить 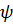. Затем определяют интегралы, входящие в формулу (18), и 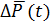при заданном 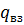. Вычислительные операции повторяют при других меньших значениях 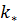, для получения зависимости .

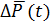Дебит нефти находят по формуле:

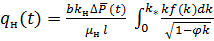(19)

а дебит воды — по формуле:

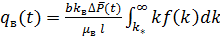(20)

В радиальном случае при поршневом вытеснении нефти водой из отдельного слоя вместо уравнения (2) будем иметь:

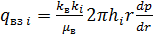(21)

Пусть в некоторый момент времени фронт вытеснения нефти водой в i- м слое дошел до радиуса 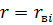, где пластовое давление равно 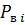Тогда, интегрируя (21) от радиуса скважины до радиуса 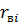, получим:

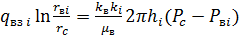(22)

В области 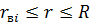т. е. впереди фронта вытеснения, движется нефть с тем же расходом 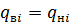, так что аналогично (22) имеем:

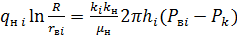(23)

Из (22) и (23):

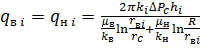(24)

Аналогично (2) для i- гo пропластка:

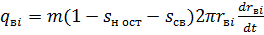(25)

Приравнивая правые части (24) и (25) и опуская индекс i, получим:

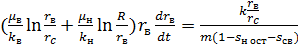(26)

Обозначим 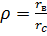и проинтегрируем (26) при 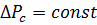. Тогда

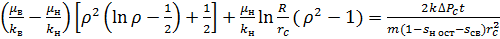(27)

Теперь можно найти время 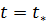, соответствующее началу обводнения пропластка с абсолютной проницаемостью .

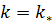Полагая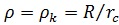, получим:

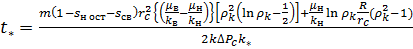(28)

Из формулы (28):

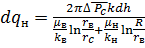(29)

Интегрируя (29), как и для прямолинейного случая, при 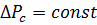имеем:

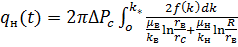(30)

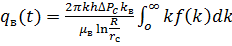. (31)

Для вычисления интеграла (30) в подынтегральное выражение следует подставить 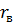, из формулы (27). Поэтому в общем случае 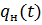необходимо определять, по-видимому, численным путем с использованием ЭВМ. Однако, как и в прямолинейном случае, при 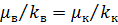вычисления упрощаются. Выражение (30) превращается в следующую формулу:

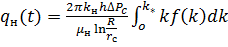(32)

Необходимо задаваться величиной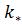, определять момент обводнения слоя с проницаемостью 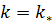по формуле (28) и в соответствии с известным вероятностно-статистическим законом распределения абсолютной проницаемост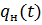и и .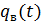

Пример 1. Нефтяной пласт в элементе однорядной схемы разработки длиной l =500 м, шириной b=500 м и толщиной h=10 м разрабатывается с применением заводнения. Пористость пласта m=0,25, вязкость нефти в пластовых условиях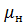=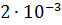Па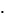с, вязкость воды 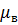=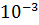Па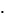с. Пласт неоднороден по толщине и может быть представлен моделью слоисто-неоднородного пласта с гамма- распределением абсолютной проницаемости. Плотность распределения соответствует 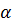=2. Поэтому

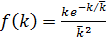(33)

Средняя абсолютная проницаемость (математическое ожидание абсолютной проницаемости) M(k)=2 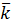=0,4 .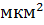

Содержание связанной воды в пласте 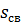=0,05, при поршневом вытеснении нефти водой из каждого отдельного слоя остаточная нефтенасыщенность в слое 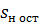=0,4. Пласт разрабатывается при постоянном перепаде давления в элементе однорядной схемы 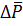= 0,2 МПа. Относительная проницаемость для нефти в незаводненных областях 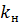=1, а относительная проницаемость для воды в заводненных зонах 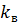=0,5.

Определим изменение во времени дебита нефти 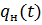и воды 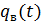, получаемых из рассматриваемого элемента однорядной системы разработки.

Прежде чем приступить к решению данного примера, отметим, что по условию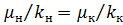. В этом случае, согласно формулам (14) и (15), имеем:

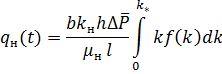
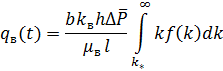
По формуле (9)

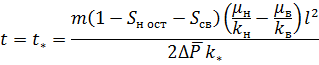
Подставляя в приведенные формулы для 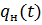и 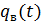данную в условии примера плотность гамма- распределения абсолютной проницаемости, получим:

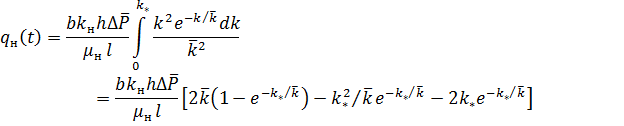
Соответственно для дебита воды:

.

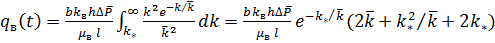Порядок расчета следующий: сначала задаемся проницаемостью 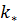, обводнившегося пропластка, затем определяем по приведенной формуле время t, обводнения этого пропластка, после чего вычисляем дебиты нефти и воды для данного времени. Расчеты повторяем аналогичным образом для других значений 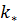и t.

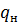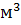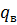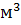На рис. 2 показан график изменения во времени дебитов нефти и воды, из которого следует, что для принятого вида распределения абсолютной проницаемости обводнение пласта в элементе системы разработки нарастает очень быстро и уже через 400 сут =15,7 /сут, а дебит воды =19 /сут.

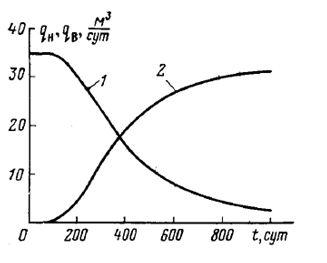
Рис. 2. График изменения во времени дебитов нефти (1) и воды(2) получаемых из элемента однорядной системы разработки.

Дата добавления: 2014-01-03