Блок деления с неподвижным остатком и сдвигом делителя вправо

Блок деления (БД) со сдвигом влево остатка при неподвижном делителе

Микроалгоритм деления чисел по первому методу имеет вид:

,

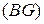
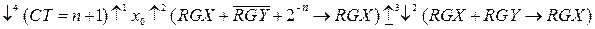
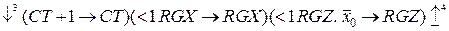
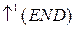где 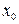– знаковый разряд RGX.

Схема БД, реализующего этот микроалгоритм, показана на рис. 8.1.

&

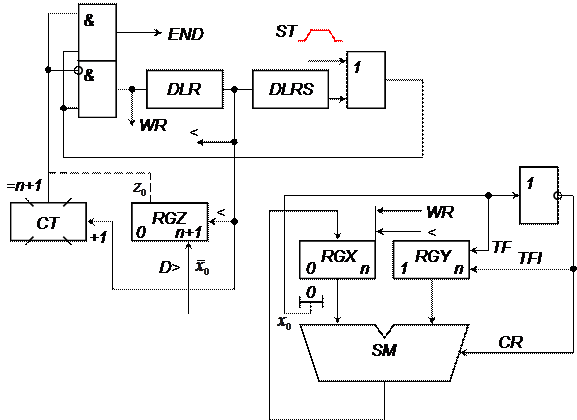Рис. 8.1. Схема блока деления, построенного по первому варианту

Для формирования сигнала END используется счетчик с периодом n + 1. С этой целью можно использовать и RGZ, если удлинить его на один разряд и записать слово 00…01 с маркерной единицей в конце. После n + 1 сдвигов маркерная единица попадает в дополнительный разряд, выход которого управляет формированием сигнала END (на рис. 8.1 показан пунктиром). В табл. 8.1 представлена цифровая диаграмма работы БД при , , .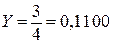

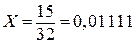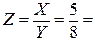
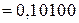Таблица 8.1

RGZ	Микрооперация	RGX	RGY
00,00000	– Y	00,01111 11,010000 11,10111	Y = 0,11000 – Y = 1,01000
00,00000	< Y	11,01110 00,110000 00,00110
00,00001	< – Y	00,01100 11,010000 11,10100
00,00010	< Y	11,01000 00,110000 00,00000
00,00101	< – Y	00,00000 11,010000 11,01000
00,01010	< Y	10,10000 00,110000 11,01000
00,10100	< END	10,10000

Из табл. 8.1 видно, что после четвертого вычитания в регистре RGX образовался нуль и далее все последующие цифры 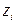частного равны нулю. Это значит, что в дальнейшем необходимо производить только сдвиги, а операции вычитания можно опустить.

Отличие блока деления, построенного по второму методу (рис. 8.2), от рассмотренного выше, состоит в том, что все регистры должны быть с внутренней задержкой. Кроме того, регистры RGX, RGY и сумматор должны иметь удвоенное число разрядов. При этом сдвиг осуществляется только в RGY и RGZ. Так как результат вычитания (остаток) неподвижен, то операцию вычитания можно совместить со сдвигом. Аппаратурные затраты на построение такого БД можно значительно сократить, если длину RGX, RGY и SM сократить до n + l разрядов. Величина l определяется из условия 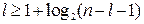, поскольку именно такое количество разрядов необходимо для того, чтобы погрешность от отбрасывания младших разрядов остатка и делителя не превысила половины веса младшего разряда результата. При 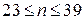получаем l = 6.

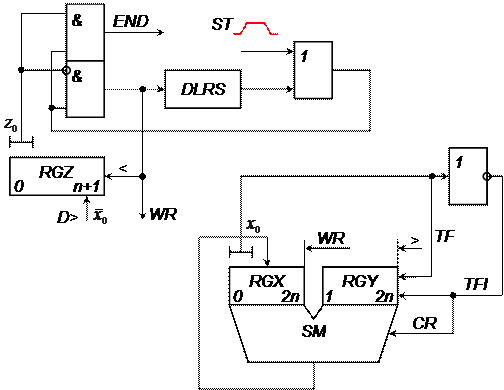Рис. 8.2. Схема блока деления, построенного по второму варианту

В БД с фиксированной запятой должна быть предусмотрена возможность фиксации переполнения разрядной сетки. Это осуществляется путем формирования сигнала совпадения 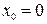с сигналом первого такта деления, который можно получить, дешифрируя нулевое состояние CT или состояние 00…01 регистра RGZ.

Дата добавления: 2014-01-03