Алгоритм деления чисел в дополнительном коде со сдвигом остатка

Основные методы деления нетрудно приспособить для выполнения операций с дополнительными кодами. Алгоритм деления со сдвигом остатка в этом случае имеет вид:

1. По знаку 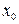делимого и знаку 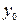делителя определить знак 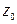частного. В качестве первого остатка взять делимое.

2. Если знаки очередного остатка и делителя совпадают, то из остатка вычесть делитель, в противном случае прибавить его к остатку. Полученный результат является новым остатком.

3. Если знаки остатка и делителя совпадают, то очередная цифра частного равна 1; если знаки не совпадают, то цифра частного равна нулю.

4. Удвоить остаток.

5. Повторить n + 1 раз пункты 2 – 4.

Рассмотрим пример. Пусть 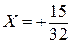, , 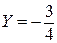тогда 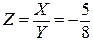, а цифровая диаграмма деления будет соответствовать табл. 8.2. Конец операции здесь определяется по маркерной 1 в RGZ.

Таблица 8.2

RGZ	Микрооперация	RGX	Такты	RGY
000,00011	+ Y	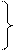00,01111 11,010000 1 T 11,10111	Y = 1,01000 – Y = 0,11000
000,00111	< – Y	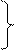11,01110 00,110000 2 T 00,00110
000,01110	< + Y	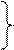00,01100 11,010000 3 T 11,10100
000,11101	< – Y	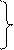11,01000 00,110000 4 T 00,00000
001,11010	< + Y	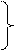00,00000 11,010000 5 T 11,01000
011,10101	< – Y	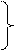10,10000 00,110000 6 T 11,01000
111,01011	< END	10,10000

Как видно из примера, результат деления получился с погрешностью в 1 младшего разряда. Аналогичная ситуация имеет место всегда, когда в процессе деления на отрицательный делитель встречается остаток, равный нулю. Действительно, согласно алгоритму при делении нуля на отрицательный делитель получается группа единиц, в то время как в данном случае должна формироваться группа нулей. Устранить этот недостаток можно двумя способами. Если вычисляется n + 1 цифра после запятой, после чего производится округление, то правильный результат получается автоматически. Если же операция округления не предусмотрена, то необходимо фиксировать схемой совпадения момент появления нулевого остатка при отрицательном делителе, и в очередной разряд частного записывать 1, а во все последующие – нули.

Таким образом БД, работающие в дополнительном коде, как по структуре, так и по аппаратным затратам и быстродействию равноценны БД, работающим в прямых кодах.

Дата добавления: 2014-01-03