Агрегатная форма индексов. Средние из индивидуальных индексов

Построение различных видов и форм индексов покажем на условных примерах.

Имеются следующие данные по ТОО «Зуня» за январь и февраль 2012 года:

товары	январь	февраль
Цена за 1кг., тенге (р0)	Количество проданных товаров, тонн,(q0)	Цена за 1кг., тенге (р1)	Количество проданных товаров, тонн,(q1)
Морковь				3,5
свекла		1,5		1,6
капуста				1,8

Требуется ответить на следующие вопросы:

1. Как изменилась цена по каждому виду товаров?

2. Как изменилось количество проданных товаров по каждому виду?

3. Как изменился товарооборот по каждому виду товаров?

4. Как изменились цены в среднем по всем товарам?

5. Как изменилось количество всех проданных товаров?

6. Как изменился товарооборот по всем товарам?

7. Определите экономию или дополнительные затраты населения произошедшие за счет:

а)изменения цен

б)изменения количества потребляемых товаров

в) обоих факторов вместе.

Первоначально определим модель взаимосвязи показателей:

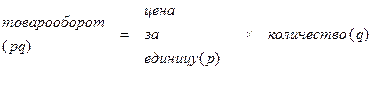
Введем условные обозначения: р₀, р₁ –цена за единицу товара соответственно в базисном и отчетном периодах; q₀, q₁ –количество проданных товаров соответственно в базисном и отчетном периодах (физический объем реализации, физический объем товарооборота).

1. Найдем индивидуальные индексы цен:

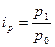
По моркови:

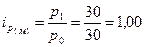-цена не изменилась

По свекле:

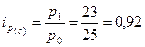- цена снизилась на 8%.

По капусте:

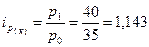- цена возросла на 14,3%.

2. Найдем индивидуальные индексы количества (физического объема продаж):

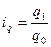
По моркови:

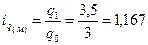- количество продаж возросло на 16,7%.

По свекле:

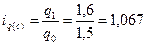- количество продаж возросло на 6,7%.

По капусте:

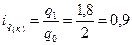- количество продаж снизилось на 10%.

3. Найдем индивидуальные индексы товарооборота:

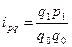
По моркови:

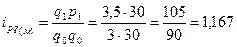-товарооборот возрос на 16,7%.

Нетрудно заметить что данную дробь можно представить в виде произведения индивидуальных индексов, которая называется взаимосвязь индивидуальных индексов и имеет большое практическое значение:

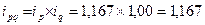
То есть увеличение товарооборота на 16,7% произошло только за счет ценового фактора.

Следовательно, по свекле:

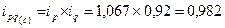
То есть, увеличение цены на 6,7% и снижение количества продаж на 8% привели к снижению товарооборота на 1,8%.

По капусте:

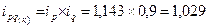- товарооборот возрос на 2,9%, за счет увеличения цены на 14,3% и снижения объема продаж на 10%.

4. Сводный индекс цен покажет их изменение по всем товарам:

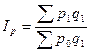
Построение такой формулы (агрегатной) объясняется прежде всего тем, что цены (это средние величины) обычным способом не суммируются. Преодолеть это поможет их взвешивание по количеству проданных товаров, взяв его неизменным (чтобы устранить влияние количественного фактора) на уровне отчетного периода. Этот индекс также называется индекс цен Пааше. Он получил широкое распространение в отечественной статистике. Подставим данные в формулу:

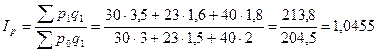
То есть цены по всем товарам возросли в среднем на 4,6%.

5. Сводный индекс количества (физического объема товарооборота) показывает как изменилось количество продаж или например, объем потребления. Построение этой формулы также объясняется несуммарностью количества, а устранить влияние ценового фактора можно взяв цены неизменными, но на уровне базисного периода:

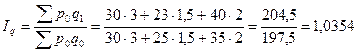
Следовательно, количество проданных товаров возросло в среднем на 3,5%

6.Сводный индекс товарооборота можно найти отношением товарооборота по всем товарам в отчетном периоде к аналогичной сумме в базисном периоде:

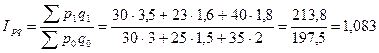
Товарооборот возрос на 8,3%. За счет увеличения цен в среднем на 4,5% и увеличения количества на 3,5%.

Между рассчитанными сводными индексами существует взаимосвязь:

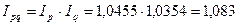
Или в виде произведения агрегатных индексов:

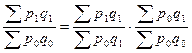
Следовательно, зная изменения двух показателей можно найти изменение третьего, даже не зная абсолютных величин самого явления.

7.Определить абсолютные суммы влияния факторов на результативный показатель, можно вычитанием из числителя – знаменателя соответствующего индекса.

Так абсолютный прирост (снижение) товарооборота за счет изменения цен можно найти следующим образом:

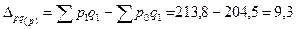тыс. тенге

Следовательно, для продавца данная сумма является приростом, а для населения дополнительными затратами.

Абсолютный прирост (снижение) товарооборота за счет изменения количества можно найти аналогично:

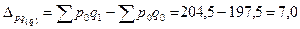тыс. тенге

Следовательно, для продавца данная сумма также является приростом, а для населения дополнительными затратами.

Абсолютный прирост (снижение) товарооборота за счет обоих факторов можно найти:

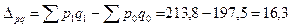тыс. тенге

Или как сумма факторов:

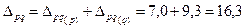тыс. тенге

Следует заметить, что в литературе рекомендуются и на практике используются другие индексы. Индекс цен с весами отчетного периода (Пааше) занижает реальное изменение цен, если снижается количество при возрастании цен, а если структура остается неизменной, то считается целесообразным использовать в качестве весов количество базисного периода, следовательно индекс цен будет иметь вид:

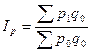- индекс цен Ласпейреса

Но как указывалось выше, главное условие применения индексного метода – наличие взаимосвязи между показателями и, следовательно между индексами. Следовательно и индекс цен Ласпейреса должен быть увязан в систему:

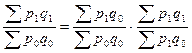
Оба варианта систем индексов имеют место на практике и в зависимости от исходных данных применяется тот или иной способ.

«Идеальным» индексом цен считается индекс цен Фишера, хотя с ним увязка индексов в систему не имеет места, но в международной практике он получил распространение:

На практике в целом ряде случаев могут быть известны не абсолютные значения индексируемых показателей, а их относительные изменения. Например, могут быть известны изменения уровней цен или себестоимости или заработной платы по категориям персонала. В таких случаях агрегатный индекс можно рассчитать косвенным путем, используя взвешенную среднюю из индивидуальных индексов, если известен размер результативного показателя за отчетный или базисный период.

При выборе весов для таких индексов следует иметь ввиду, что средний индекс должен быть тождественен агрегатному, который является основной формой индекса. Так, индекс цен можно рассчитать как средний гармонический индекс цен, основной формой которого является агрегатный индекс Пааше:

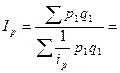
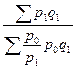
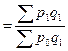
Или средневзвешенный индекс физического объема:

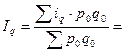
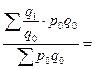
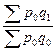
Применение той или иной формулы построения индексов зависит и от имеющейся в нашем распоряжении информации.

Дата добавления: 2014-01-03