
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные расчетные схемы
|
|
|
|
Вычисление площадей плоских фигур
Лекция № 7, ВА-1, матан, 2 семестр
Тема. Геометрические и механические приложения определенного интеграла. Вычисление площадей плоских фигур, объемов тел вращения, пути, пройденного телом при неравномерном движении
Определенный интеграл применяется при решении разнообразных практических задач. Одной из таких задач является задача вычисления площади плоской фигуры. Разбору решения таких задач посвящен настоящий параграф.
Рассмотрим расчетные схемы.
10. Фигура представляет собой криволинейную трапецию, ограниченную сверху линией, 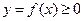 на отрезке
на отрезке 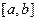 , снизу осью
, снизу осью 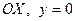 , с боков прямыми
, с боков прямыми 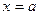 ,
, 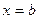 (рис. 1.1).
(рис. 1.1).
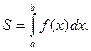 (2.1)
(2.1)
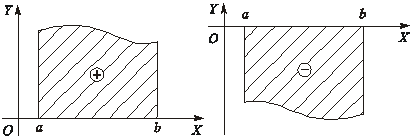
Рис. 1.1 Рис. 1.2
20. Фигура на отрезке 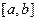 расположена ниже оси
расположена ниже оси 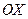 . Функция
. Функция 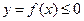 (рис. 1.2), интеграл (2.1) также не больше нуля и по модулю равен площади криволинейной трапеции. Площадь вычисляем по формуле:
(рис. 1.2), интеграл (2.1) также не больше нуля и по модулю равен площади криволинейной трапеции. Площадь вычисляем по формуле:
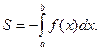 (1.2)
(1.2)
30. Функция 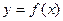 на отрезке
на отрезке 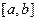 изменяет знак конечное число раз, (рис.1.3).
изменяет знак конечное число раз, (рис.1.3).
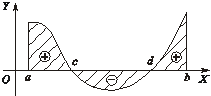 |
Рис. 1.3
Интеграл по отрезку 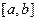 разбиваем на сумму интегралов по частичным отрезкам, где функция не изменяет знак. Интеграл положителен, на отрезках, где
разбиваем на сумму интегралов по частичным отрезкам, где функция не изменяет знак. Интеграл положителен, на отрезках, где 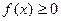 и отрицателен, где
и отрицателен, где 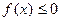 . Интеграл по отрезку
. Интеграл по отрезку 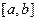 даст алгебраическую сумму площадей частей фигуры. Для получения суммы площадей в обычном смысле нужно вычислить интеграл:
даст алгебраическую сумму площадей частей фигуры. Для получения суммы площадей в обычном смысле нужно вычислить интеграл:
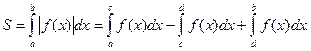 (1.3)
(1.3)
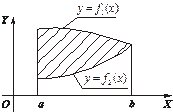 40. Фигура ограничена кривыми
40. Фигура ограничена кривыми 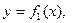
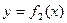 и ординатами
и ординатами 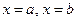 (рис.1.4).
(рис.1.4).
Рис. 1.4
При условии 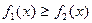 площадь ее вычисляем по формуле:
площадь ее вычисляем по формуле:
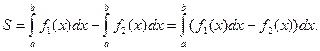 (1.4)
(1.4)
1.2. Примеры вычисленя площадей
плоских фигур
Проиллюстрируем применение формул (1.1) – (1.4) к решению практических задач.
Задача 1.1. Найти площадь фигуры, ограниченной линиями:
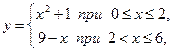
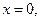
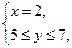
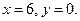
Решение. Фигура изображена на рис. 1.5.
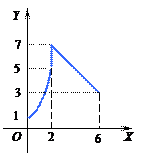 |
Рис. 1.5
Функция 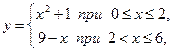 ограничена, имеет одну точки разрыва (
ограничена, имеет одну точки разрыва (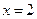 ), поэтому интегрируема. Площадь фигуры равна сумме двух определенных интегралов с пределами интегрирования: первый –
), поэтому интегрируема. Площадь фигуры равна сумме двух определенных интегралов с пределами интегрирования: первый – 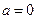 и
и 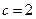 , второй –
, второй – 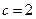 и
и 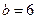 . (Интеграл от данной функции вычислен в лекции № 5).
. (Интеграл от данной функции вычислен в лекции № 5).
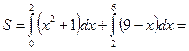
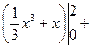
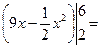
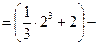
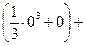
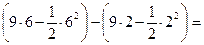
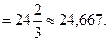
Задача 1.2. Найти площадь фигуры, ограниченной гиперболой 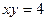 и прямой
и прямой 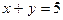 (рис. 1.6).
(рис. 1.6).
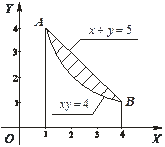
Рис. 1.6
Решение. Для построения фигуры найдем точки пересечения гиперболы и прямой. Решим систему уравнений:
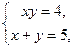
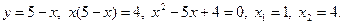
Отсюда 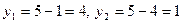 , и получаем точки пересечения гиперболы и прямой:
, и получаем точки пересечения гиперболы и прямой: 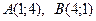 . Рассматриваемая фигура представлена на рис 1.6. Пределы интегрирования:
. Рассматриваемая фигура представлена на рис 1.6. Пределы интегрирования: 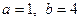 , прямая
, прямая 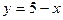 на отрезке
на отрезке 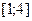 расположена выше гиперболы
расположена выше гиперболы 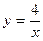 , поэтому по формуле (1.4) получаем:
, поэтому по формуле (1.4) получаем:
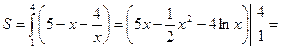
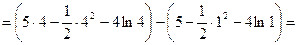
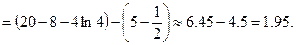
Задача 1.3. Найти площадь фигуры, ограниченной синусоидой и осью 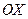 на отрезке
на отрезке 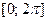 .
.
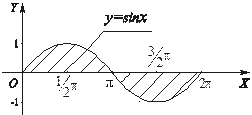 |
Рис. 1.7
Фигура расположена выше оси 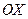 на интервале
на интервале 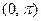 и ниже оси
и ниже оси 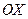 на интервале
на интервале 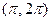 (рис. 1.7). Поэтому воспользуемся формулой (1.3):
(рис. 1.7). Поэтому воспользуемся формулой (1.3):
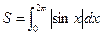 .
.
Разобьем фигуру на две части: от 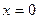 до
до 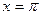 и от
и от 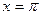 до
до 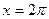 . Так как на промежутке
. Так как на промежутке 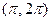
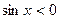 , то на нем
, то на нем 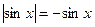 , и последний интеграл представлен в виде:
, и последний интеграл представлен в виде:
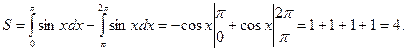
Задача 1.4. Найти площадь фигуры, ограниченной линиями:
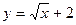
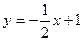
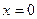
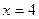
Фигура представлена на рис. 1.8. Пределы интегрирования равны: 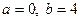 , кривая
, кривая 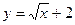 расположена выше прямой
расположена выше прямой 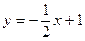 на отрезке
на отрезке 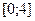 , поэтому площадь фигуры по формуле (14.4) равна:
, поэтому площадь фигуры по формуле (14.4) равна:
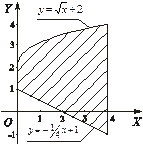 |
Рис. 1.8
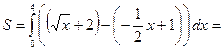
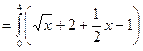
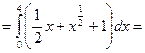
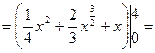
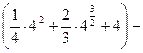
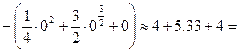 13.33.
13.33.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 429; Нарушение авторских прав?; Мы поможем в написании вашей работы!