Формулы объемов тел вращения

Вычисление объемов тел враения

Получим формулы объема тела вращения. Рассмотрим два случая.

1⁰. Тело образовано вращением вокруг оси OX криволинейной трапецией, ограниченной непрерывной кривой 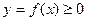, осью OX, 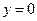и прямым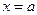и и 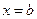. (рис. 2.1)

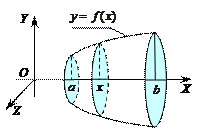Рис. 2.1

Сечение этого тела плоскостью, проведенной через точку x 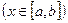и перпендикулярной оси OX, представляет собою круг с радиусом 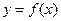. Площадь сечения круга составляет 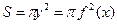, и объем тела вращения равен:

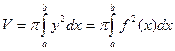. (2.1)

2⁰. Тело образовано вращением вокруг оси OY криволинейной трапецией, ограниченной непрерывной кривой 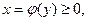отрезком 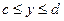и прямым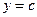и и 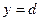(рис. 2.2).

Рис. 2.2

В этом случае объем тела выразится формулой, аналогичной формуле (2.1):

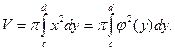(2.2)

2.2. Применение формул объемов тел
вращения к решению задач

Задача 2.1. Найти объем тела, образованного вращением фигуры, ограниченной параболой 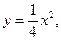отрезком 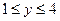и прямым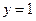и и 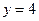вокруг оси OY (рис. 2.3).

Рис. 2.3

Решение. Уравнение параболы разрешим относительно переменной x:

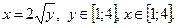
Подставим полученное значение x в формулу (2.1), получим:

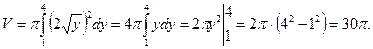
Задача 2.2. Найти объем тела, образованного вращением фигуры, ограниченной гиперболой 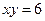и прямой 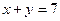вокруг оси 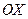(рис. 2.4).

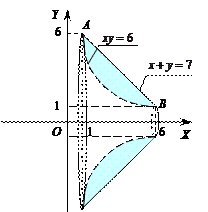Рис. 2.4

Решение. Для построения фигуры, образующей тело вращения, найдем точки пересечения гиперболы и прямой. Для того решим систему уравнений:

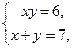
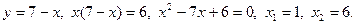
Отсюда 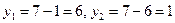, и получаем точки пересечения гиперболы и прямой: 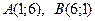. Тело вращения представлено на рис 2.4.

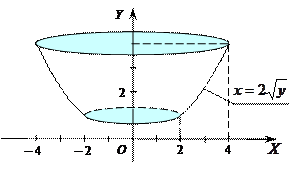
Тело вращения – «воронка», ограниченная снаружи прямолинейной конической поверхностью с образующей, определяемой уравнением:

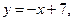(2.3)

и криволинейной конической поверхностью внутри, определяемой уравнением:

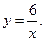(2.4)

Объем «воронки» равен разности объемов двух конусов – прямолинейного конуса и криволинейного. Пределы интегрирования: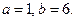

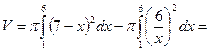
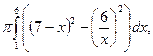
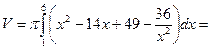
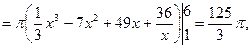
Ответ.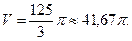

3. Применение определенного интеграла
к вычислению пути, пройденного телом
при неравномерном движении

Ставится задача. Тело движется по прямой с переменной скоростью 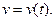Определим путь, пройденный телом за промежуток времени от 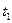до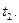

Решение. Известно, что при прямолинейном движении скорость является производной пути по времени:

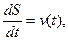или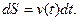

Из последнего равенства следует:

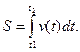(3.1)

Формула (3.1) выражает путь, пройденный телом за промежуток времени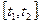

Применим полученную формулу к решению конкретной задачи.

Задача 2.1. Определить путь, пройденный телом при свободном падении с нулевой начальной скоростью за промежуток времени от момента 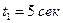до момента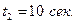

Решение. Скорость свободного падения с нулевой начальной скоростью выражается формулой 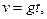где 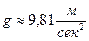– ускорение свободного падения. Подставляя это выражение скорости в формулу (3.1), получаем:

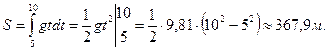
Дата добавления: 2014-01-03