Значения нормальной функции распределения Ф(х),

У. ед.

Дни

Рис.2.1. Прогноз текущего расхода деталей на складе ():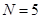

1 - исходные данные; 2 - уравнение тренда; 3,3- границы

интервального прогноза; 4 - время расхода запаса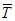

Для учета возможных нарушений срока поставки необходимо оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой.

По одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки. Однако можно предположить, что выявленная тенденция расхода запаса, формула (1.2), сохранится.

В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой:

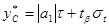, (2.6)

где 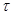- параметр, характеризующий количество дней задержки поставки заказа.

Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой 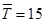дней, т.е. на 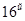день.

По формуле (2.6) находим:

.

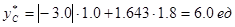Аналогично при 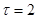(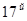день) .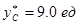

Допустим, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения.

Определим вероятность отсутствия дефицита по формуле:

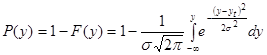, (2.7)

где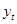- уравнение тренда, формула (2.1);

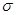- среднее квадратическое отклонение, формула (2.4).

Сделаем в интеграле замену переменной:

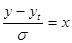(2.8)

и приведем его к виду:

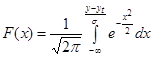. (2.9)

Для расчетов данного интеграла можно воспользоваться численными методами и ЭВМ или специальными таблицами.

Для нормальной функции распределения с параметрам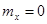и и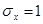

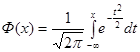. (2.10)

Очевидно, что: .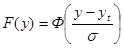

В табл.2.4 приведен ряд значений функци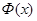и и .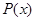

Таблица 2.4

Дата добавления: 2014-01-03