Вероятности Р(х) и параметра х

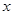
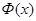
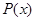
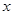
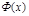
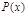
0,00	0,50	0,50	-1,280	0,10	0,90
-0,125	0,45	0,55	-1,405	0,08	0,92
-0,253	0,40	0,60	-1,555	0,06	0,94
-0,385	0,35	0,65	-1,645	0,05	0,95
-0,525	0,30	0,70	-1,75	0,04	0,96
-0,675	0,25	0,75	-2,05	0,02	0,98
-0,842	0,20	0,80	-2,30	0,01	0,99
-1,037	0,15	0,85	-3,10	0,001	0,999

Между параметрам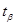и и 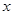, а также 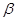и 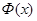существует соотношение:

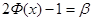. (2.11)

На рис.2.2 приведены графики нормальной функции распределения и плотности нормального распределения.

Появление дефицита означает, что текущая величина запаса на складе равна нулю, т.е. .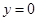

Для определения вероятности отсутствия дефицита необходимо:

по формуле (2.8) рассчитать ;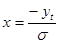

по табл.2.4 с помощью 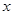найти .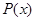

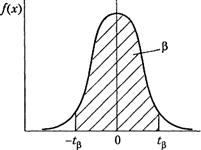
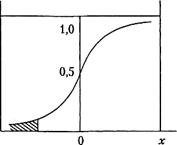
Рис.2.2. Нормальный закон распределения:

а) - плотность распределения; б) - функция распределения

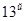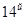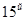Для рассматриваемого примера рассчитаем вероятности отсутствия дефицита деталей на складе на , и дни.

Для 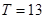получаем: ; .

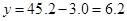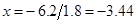По табл.2.4 находим 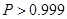, т.е. вероятность дефицита ничтожно мала.

Для 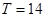получаем: ; ; .

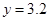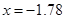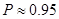Для 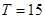получаем: .

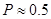Определим ошибку прогноза среднего времени 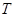, поскольку имеются реальные данные о текущем расходе в табл.2.1:

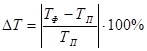, (2.12)

где 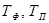- соответственно фактическая и прогнозная продолжительность цикла.

Подставив значения в (2.12), находим:

.

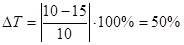Ошибка прогноза велика, но это закономерно, так как нарушено одно из эмпирических правил экстраполяционного прогнозирования: между предпрогнозным периодом 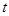и периодом упреждения (прогноза) 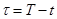должно соблюдаться соотношение:

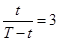. (2.13)

Если следовать соотношению (2.13), то при 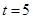допустимая величина времени прогноза:

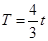. (2.14)

Следовательно, величина надежного прогноза соответствует 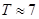дней и период упреждения составляет 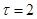дня.

Дата добавления: 2014-01-03