Свойства полюсов и поляр

1. Если точка и прямая инцидентны, то их поляра и полюс так же инцидентны.

2. Для всякой прямой существует единственный полюс относительно овальной квадрики.

3. Если точка Q лежит на поляре точки Р, относительно овальной квадрики G, то поляра точки Q проходит через точку Р.

4. Если точка А внешняя по отношению к квадрики G, то её поляра проходит через точки касания касательных проведенных из точки А к квадрике.

Определение 8.5. Отображение, при котором каждой точке проективной плоскости ставится в соответствии её поляра относительно квадрики, а каждой прямой её полюс называется полярной корреляцией.

Определение 8.6. Фигура называется автополярной если её полярный образ совпадает с ней.

Определение 8.7. Автополярным трехвершинником называется трехвершинник, у которого каждая вершина является полюсом противоположной стороны.

Трехвершинник бывает автополярным лишь относительно некоторой овальной квадрики. Овальная квадрика имеет бесконечное множество автополярных трехвершинников.

Теорема 8.8. Для того чтобы уравнение овальной квадрики не содержало членов с произведением координат необходимо и достаточно, чтобы координатный трехвершинник был автополярным относительно данной квадрики, т.е.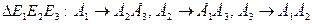

Дата добавления: 2014-01-03