Постановка задачи

Поиск минимума

Лекция №7

Постановка задачи на поиск минимума выглядит следующим образом. Здесь и в дальнейшем будем искать минимум, при этом задача по поиску максимума легко может быть определена путем переформулировки задачи на минимум, заменой соответствующих неравенств на противоположные, inf на sup и соответственно min на max. Пусть имеется множество X, входящее в некоторое метрическое пространство. На множестве X определена скалярная функция F = F (x), x Î X. Говорят, что F (x) имеет локальный минимум в точке 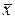, если существует конечная e -окрестность этой точки, на которой выполняется

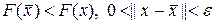. (1)

Функция может иметь множество локальных минимумов, если же выполняется условие

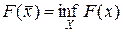, (2)

то говорят о достижении функцией абсолютного минимума на множестве X.

Необходимо наложить некоторые условия на множество X и вид функции F. Функция F должна быть хотя бы непрерывной (либо кусочно-непрерывной), т.к. иначе построить какой-либо разумный алгоритм поиска, кроме поиска минимума путем перебора, не остается. Если множество X — числовая ось, то задачи (1), (2) являются задачами поиска минимума функции одной вещественной переменной. Если X является n -мерным векторным пространством, то задачи (1), (2) являются задачами на минимум функции n переменных. Если X является некоторым функциональным пространством, то задача (1) является задачей минимизации соответствующего функционала.

Поиск абсолютного минимума состоит из нахождения всех локальных минимумов и выбора среди них минимального, т.е. задача (2) сводится к задаче (1). Поэтому в дальнейшем в основном будем заниматься решением задачи (1), т.е. поиском локальных минимумов.

Если множество X есть числовая ось, а функция F имеет непрерывную производную, то, как известно, решения задачи (1) являются корнями уравнения:

F ¢(x) = 0. (3)

Если множество X есть n -мерное векторное пространство, то решения задачи (1) удовлетворяют системе уравнений вида:

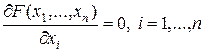. (3¢)

Для поиска минимума и вообще точек экстремума можно в принципе численно решить уравнения (3), (3¢). Однако в этом разделе будут рассмотрены прямые методы решения задачи (1).

Пусть множество X выделено в исходном пространстве с помощью некоторых условий типа равенств. В этом случае задачу (1) называют задачей на условный минимум (экстремум). Методом неопределенных множителей Лагранжа такие задачи можно свести к задаче на безусловный экстремум.

Задачу поиска минимума называют детерминированной, если погрешностью в определении функции F (x) можно пренебречь. Если погрешностью пренебречь нет возможности, задача называется стохастической. Здесь в основном рассматриваются детерминированные задачи.

Дата добавления: 2014-01-03