Метод парабол

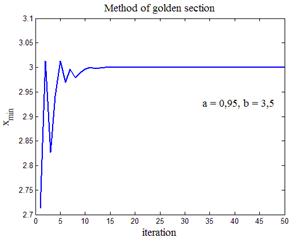
Метод золотого сечения является надежным, но медленным. Так, в предыдущем примере поиска минимума для достижения точности 10 десятичных знаков потребовалось 50 ¸ 60 итераций. Если функция дифференцируема, то возможно использовать гораздо более быстрые методы отыскания экстремума, основанные на решении уравнения F ¢(x) = 0. Если функция имеет вторую производную и в точке экстремума F ¢¢(x) > 0, то это, как известно, минимум, если F ¢¢(x) < 0, то — максимум.

Разложим функцию F (x) в ряд Тейлора в точке x_s, оставляя первые три члена ряда, тогда

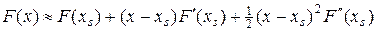. (11)

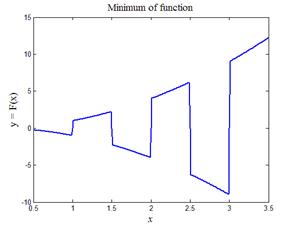
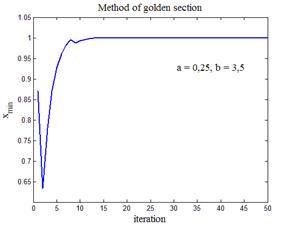
Рис.3,а. График минимизируемой функции	Рис.3,б. Выход на первый локальный минимум (x min = 1)
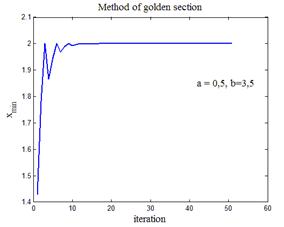
Рис.3,б. Выход на второй локальный минимум (x min = 2)	Рис.3,б. Выход на третий локальный минимум (x min = 3)

Согласно (11), исходная функция аппроксимирована параболой, которая принимает экстремальное значение (либо минимум, либо максимум) в точке

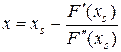. (12)

Если положить в (12) x = x_{s +1} получим итерационный процесс, который при удачном выборе начального приближения быстро сходится к точке экстремума функции. Поскольку итерационный процесс (12) ньютоновского типа, постольку он, как установлено выше, сходится квадратично.

Часто как первая, так и вторая производные функции выглядят громоздко. В этом случае производные возможно заменить соответствующими конечными разностями. Для первой производной выберем центральную разность, а для второй — симметричную вторую разность. В итоге получим:

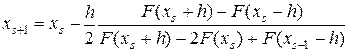. (13)

Формула (13) может быть также получена путем нахождения положения экстремума интерполяционной параболы, построенной по трем точкам 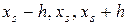. Именно поэтому итерационный процесс (13) называется методом парабол.

Выведем формулу (13). Запишем интерполяционную параболу: y = a + bx + cx ². Для нахождения неизвестных коэффициентов a, b, c составим систему уравнений:

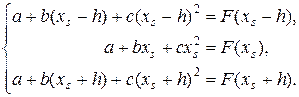(14)

Решим систему уравнений (14), используя аналитические средства вычислений в MATLAB. Кроме того, найдем значение аргумента x, в котором парабола y = a + bx + cx ²достигает экстремального значения. На листинге_№2 приведен код соответствующей программы.

Листинг_№2

%Программа нахождения коэффициентов

%интерполяционной параболы в методе

%парабол нахождения экстремальных точек

%очищаем рабочее пространство

clear all

%определяем символические переменные

syms xs h

%определяем значения интерполируемой функции

%в точках xs-h, xs и xs+h соответственно

syms Fsm Fs Fsp

%определяем матрицу линейной системы

%уравнений (14) относительно неизвестных a, b, c

A=[1 xs-h (xs-h)^2;1 xs xs^2;1 xs+h (xs+h)^2];

%определяем правую часть r линейной

%системы уравнений

r=[Fsm;Fs;Fsp];

%символически решаем линейную систему уравнений

abc=A\r;

%искомое положение точки экстремума параболы xps

%находится, как известно, из соотношения -b/2c

xps=-abc(2)/(2*abc(3))

Итог работы кода программы листинга_№2 дает следующее выражение:

xps =

1/2*(-4*xs*Fs+2*xs*Fsp+2*xs*Fsm-h*Fsp+Fsm*h)/(-2*Fs+Fsp+Fsm)

Это выражение, как нетрудно проверить, полностью совпадает с уравнением (14), когда xps = x_{s +1}, Fsm = F (x_s - h), Fs = F (x_s), Fsp = F (x_s + h).

Рассмотрим пример работы метода парабол. Возьмем функцию F следующего вида: F (x) = cos(p x ²), экстремумы которой, как нетрудно проверить, находятся в точках 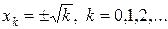При изучении метода парабол будем стартовать с разных начальных данных и посмотрим на характер сходимости к экстремумам изучаемой функции. На листинге_№3 приведен код соответствующей программы.

Листинг_№3

%Программа, иллюстрирующая работу метода

%парабол на примере поиска положений

%экстремумов функции F(x)=cos(pi*x^2)

%очищаем рабочее пространство

clear all

%определяем функцию, значения экстремумов

%которой определяются

F=@(x)cos(pi*x^2);

%определяем параметр h метода парабол

h=1e-4;

%определяем число итераций в методе парабол

iterm=10;

%задаем набор начальных значений

x0=-1.6:0.05:1.6;

%организуем цикл расчетов по методу парабол

%стартуя с каждого начального значения

for i=1:length(x0)

xs=x0(i);

iter=1; x(1)=xs;

%организуем цикл итераций метода парабол

while iter<iterm

xs=xs-0.5*h*((F(xs+h)-F(xs-h))/...

(F(xs+h)-2*F(xs)+F(xs-h)));

iter=iter+1; x(iter)=xs;

end

%наносим очередной график зависимости

%значений итераций от номера итераций

plot(1:iter,x);

hold on

end

На рис.4 приведен итог работы кода программы листинга_№3. Рис.4 демонстрирует, во-первых, очень быструю сходимость (в пределах 10 итераций достигается точность 8 знаков после запятой, кроме нулевой точки) к одному из локальных экстремумов 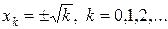функции F (x) = cos(p x ²), во-вторых, график иллюстрирует довольно сложную зависимость между начальным приближением и выходом на то или иное экстремальное значение. На рис.4 представлено 65 расчетов методом парабол при выборе различных начальных данных. Точнее говоря, был рассмотрен отрезок [-1,6;1,6], на котором выбрана равномерная сетка с шагом 0,05, т.е. начальные данные x 0 выбирались согласно формуле: x 0 _i = -1,6 + 0,05(i - 1), i = 1,…,65. При этом было найдено 13 локальных минимумов: 0, ±1, ±Ö2, ±Ö3, ±Ö5, ±Ö6, ±.

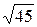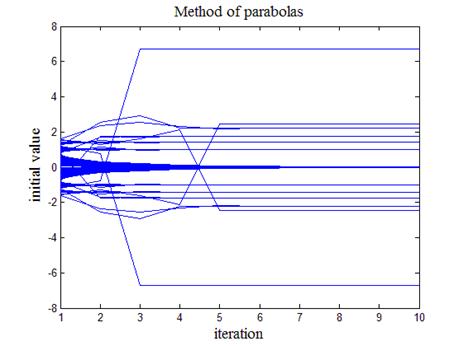
Рис.4. Демонстрация характера связи начальных значений с
экстремальными точками изучаемой функции

Дата добавления: 2014-01-03